
设两非零向量e1和e2不共线.
(1)如果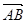 =
= +
+  ,
,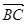 =2
=2  +8
+8  ,
,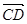 =3(
=3( -
- ),求证:A、B、D三点共线;
),求证:A、B、D三点共线;
(2)试确定实数k,使k  +
+  和
和 +k
+k  共线;
共线;
(3)若|  |=2,|
|=2,|  |=3,
|=3,  与
与 的夹角为60°,试确定k的值,使k
的夹角为60°,试确定k的值,使k  +
+  与
与 +k
+k  垂直.
垂直.
(1)见解析;(2)k=±1.;(3)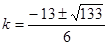
【解析】
试题分析:(1)证明: =6(
=6(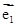 +
+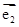 )=
)=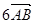 ,
,
∴ ∥
∥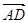 ,
, 与
与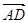 有公共点A.
有公共点A.
∴A、B、D三点共线.
(2)∵k 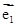 +
+ 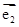 和
和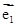 +k
+k 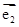 共线,
共线,
∴存在λ使k 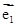 +
+ 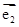 =λ(
=λ(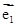 +k
+k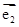 ),
),
即(k-λ) 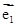 +(1-λk)
+(1-λk) 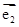 =0.
=0.
∵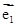 与
与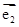 为非零不共线向量,
为非零不共线向量,
∴k-λ=0且1-λk=0.∴k=±1.
(3)由(k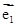 +
+ 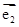 )·(
)·(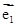 +k
+k 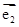 )=0,
)=0,
k| 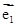 |2+(k2+1)
|2+(k2+1) 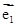 ·
·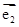 +k|
+k|
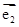 |2=0,得
|2=0,得
k×22+(k2+1)×2×3×cos60°+k×32=0
 4k+3k2+3+9k=0
4k+3k2+3+9k=0 3k2+13k+3=0,
3k2+13k+3=0,
∴ 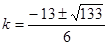 .
.
考点:本题主要考查空间向量的线性运算、向量数量积的应用。
点评:两向量垂直,它们的数量积为0。两向量共线,对应坐标成比例。具有一定的综合性。


科目:高中数学 来源: 题型:
| AB |
| BC |
| CD |
查看答案和解析>>
科目:高中数学 来源: 题型:
(1)如果![]() =e1+e2,
=e1+e2,![]() =2e1+8e2,
=2e1+8e2,![]() =3(e1,-e2),求证:A、B、D三点共线;
=3(e1,-e2),求证:A、B、D三点共线;
(2)试确定实数k,使ke1+e2和e1+ke2共线.
查看答案和解析>>
科目:高中数学 来源: 题型:
(1)如果![]() =e1+e2,
=e1+e2,![]() =2e1+8e2,
=2e1+8e2,![]() =3(e1-e2),求证:A、B、D三点共线;
=3(e1-e2),求证:A、B、D三点共线;
(2)试确定实数k,使ke1+e2和e1+ke2共线.
查看答案和解析>>
科目:高中数学 来源:《2.4-2.5 平面向量的数量积及平面向量的应用举例》2011年同步练习(解析版) 题型:解答题
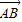 =e1+e2,
=e1+e2,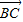 =2e1+8e2,
=2e1+8e2,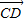 =3(e1-e2),求证:A、B、D三点共线;
=3(e1-e2),求证:A、B、D三点共线;查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com