
【题目】如图,在多面体![]() 中,底面
中,底面![]() 为菱形,
为菱形,![]() ,
,![]() ,
,![]() 平面
平面![]() ,
,![]() ,
,![]() .
.
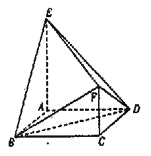
(1)若点![]() ,
,![]() 分别在
分别在![]() ,
,![]() 上,且
上,且![]() ,
,![]() ,证明
,证明![]() 平面
平面![]() .
.
(2)若平面![]() 平面
平面![]() ,求平面
,求平面![]() 把多面体
把多面体![]() 分成大、小两部分的体积比.
分成大、小两部分的体积比.
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案科目:高中数学 来源: 题型:
【题目】某企业拥有3条相同的生产线,每条生产线每月至多出现一次故障.各条生产线是否出现故障相互独立,且出现故障的概率为![]() .
.
(1)求该企业每月有且只有1条生产线出现故障的概率;
(2)为提高生产效益,该企业决定招聘名维修工人及时对出现故障的生产线进行维修.已知每名维修工人每月只有及时维修1条生产线的能力,且每月固定工资为1万元.此外,统计表明,每月在不出故障的情况下,每条生产线创造12万元的利润;如果出现故障能及时维修,每条生产线创造8万元的利润;如果出现故障不能及时维修,该生产线将不创造利润,以该企业每月实际获利的期望值为决策依据,在![]() 与
与![]() 之中选其一,应选用哪个?(实际获利=生产线创造利润-维修工人工资)
之中选其一,应选用哪个?(实际获利=生产线创造利润-维修工人工资)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】关于函数![]() 有下述四个结论:①若
有下述四个结论:①若![]() ,则
,则![]() ;②
;②![]() 的图象关于点
的图象关于点![]() 对称;③函数
对称;③函数![]() 在
在![]() 上单调递增;④
上单调递增;④![]() 的图象向右平移
的图象向右平移![]() 个单位长度后所得图象关于
个单位长度后所得图象关于![]() 轴对称.其中所有正确结论的编号是( )
轴对称.其中所有正确结论的编号是( )
A.①②④B.①②C.③④D.②④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 为实数,函数
为实数,函数![]() ,且函数
,且函数![]() 是偶函数,函数
是偶函数,函数![]()
![]() 在区间
在区间![]() 上的减函数,且在区间
上的减函数,且在区间![]() 上是增函数.
上是增函数.
(1)求函数![]() 的解析式;
的解析式;
(2)求实数![]() 的值;
的值;
(3)设![]()
![]() ,问是否存在实数
,问是否存在实数![]() ,使得
,使得![]() 在区间
在区间![]() 上有最小值为
上有最小值为![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一种作图工具如图1所示.![]() 是滑槽
是滑槽![]() 的中点,短杆
的中点,短杆![]() 可绕
可绕![]() 转动,长杆
转动,长杆![]() 通过
通过![]() 处铰链与
处铰链与![]() 连接,
连接,![]() 上的栓子
上的栓子![]() 可沿滑槽AB滑动,且
可沿滑槽AB滑动,且![]() ,
,![]() .当栓子
.当栓子![]() 在滑槽AB内作往复运动时,带动
在滑槽AB内作往复运动时,带动![]() 绕
绕![]() 转动一周(
转动一周(![]() 不动时,
不动时,![]() 也不动),
也不动),![]() 处的笔尖画出的曲线记为
处的笔尖画出的曲线记为![]() .以
.以![]() 为原点,
为原点,![]() 所在的直线为
所在的直线为![]() 轴建立如图2所示的平面直角坐标系.
轴建立如图2所示的平面直角坐标系.
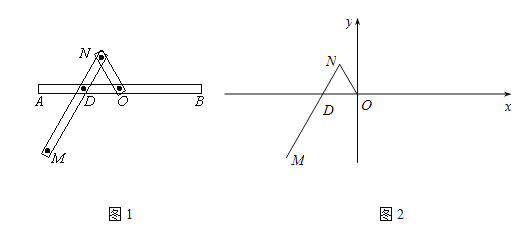
(Ⅰ)求曲线C的方程;
(Ⅱ)设动直线![]() 与两定直线
与两定直线![]() 和
和![]() 分别交于
分别交于![]() 两点.若直线
两点.若直线![]() 总与曲线
总与曲线![]() 有且只有一个公共点,试探究:
有且只有一个公共点,试探究:![]() 的面积是否存在最小值?若存在,求出该最小值;若不存在,说明理由.
的面积是否存在最小值?若存在,求出该最小值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某快递公司在某市的货物转运中心,拟引进智能机器人分拣系统,以提高分拣效率和降低物流成本,已知购买x台机器人的总成本为![]() 万元.
万元.

(1)若使每台机器人的平均成本最低,问应买多少台?
(2)现按(1)中的数量购买机器人,需要安排m人将邮件放在机器人上,机器人将邮件送达指定落袋格口完成分拣(如图).经实验知,每台机器人的日平均分拣量为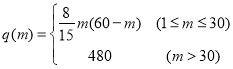 ,(单位:件).已知传统的人工分拣每人每日的平均分拣量为1200件,问引进机器人后,日平均分拣量达最大时,用人数量比引进机器人前的用人数量最多可减少百分之几?
,(单位:件).已知传统的人工分拣每人每日的平均分拣量为1200件,问引进机器人后,日平均分拣量达最大时,用人数量比引进机器人前的用人数量最多可减少百分之几?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年1月1日新修订的个税法正式实施,规定:公民全月工资、薪金所得不超过5000元的部分不必纳税,超过5000元的部分为全月应纳税所得额.此项税款按下表分段累计计算(预扣):
全月应缴纳所得额 | 税率 |
不超过3000元的部分 |
|
超过3000元至12000元的部分 |
|
超过12000元至25000元的部分 |
|
国家在实施新个税时,考虑到纳税人的实际情况,实施了《个人所得税税前专项附加扣税暂行办法》,具体如下表:
项目 | 每月税前抵扣金额(元) | 说明 |
子女教育 | 1000 | 一年按12月计算,可扣12000元 |
继续教育 | 400 | 一年可扣除4800元,若是进行技能职业教育或者专业技术职业资格教育一年可扣除3600元 |
大病医疗 | 5000 | 一年最高抵扣金额为60000元 |
住房贷款利息 | 1000 | 一年可扣除12000元,若夫妻双方在同一城市工作,可以选择一方来扣除 |
住房租金 | 1500/1000/800 | 扣除金额需要根据城市而定 |
赡养老人 | 2000 | 一年可扣除24000元,若不是独生子女,子女平均扣除.赡养老人年龄需要在60周岁及以上 |
老李本人为独生子女,家里有70岁的老人需要赡养,有一个女儿正读高三,他每月还需缴纳住房贷款2734元.若2019年11月老李工资,薪金所得为20000元,按照《个人所得税税前专项附加扣税暂行办法》,则老李应缴纳税款(预扣)为______元.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]()
![]() 经过点
经过点![]() ,
,![]() ,点
,点![]() 为椭圆
为椭圆![]() 的右顶点,直线
的右顶点,直线![]() 与椭圆相交于不同于点
与椭圆相交于不同于点![]() 的两个点
的两个点![]() 、
、![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)当![]() 时,求
时,求![]() 面积的最大值;
面积的最大值;
(3)若![]() ,求证:
,求证:![]() 为定值.
为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司举办捐步公益活动,参与者通过捐赠每天的运动步数获得公司提供的牛奶,再将牛奶捐赠给留守儿童.此活动不但为公益事业作出了较大的贡献,公司还获得了相应的广告效益.据测算,首日参与活动人数为![]() 人,以后每天人数比前一天都增加
人,以后每天人数比前一天都增加![]() ,
,![]() 天后捐步人数稳定在第
天后捐步人数稳定在第![]() 天的水平,假设此项活动的启动资金为
天的水平,假设此项活动的启动资金为![]() 万元,每位捐步者每天可以使公司收益
万元,每位捐步者每天可以使公司收益![]() 元(以下人数精确到
元(以下人数精确到![]() 人,收益精确到
人,收益精确到![]() 元).
元).
(1)求活动开始后第![]() 天的捐步人数,及前
天的捐步人数,及前![]() 天公司的捐步总收益;
天公司的捐步总收益;
(2)活动开始第几天以后公司的捐步总收益可以收回启动资金并有盈余?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com