
如图4所示的茎叶图记录了甲、乙两个小组(每小组4人)在期末考试中

的数学成绩.乙组记录中有一个数据模糊,无法确认,在图中以 表示.
表示.
已知甲、乙两个小组的数学成绩的平均分相同.
(1)求 的值;
的值;
(2)求乙组四名同学数学成绩的方差;
(3)分别从甲、乙两组同学中各随机选取一名同学,记这两名同学数学
成绩之差的绝对值为 ,求随机变量
,求随机变量 的分布列和均值(数学期望).
的分布列和均值(数学期望).
(温馨提示:答题前请仔细阅读卷首所给的计算公式及其说明.)
(本小题主要考查统计、方差、随机变量的分布列、均值(数学期望)等知识,考查或然与必然的数学思想方法,以及数据处理能力、运算求解能力和应用意识)
(1)解:依题意,得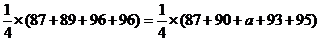 ,………………1分
,………………1分
解得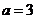 .……………………………………………………………………2分
.……………………………………………………………………2分
(2)解:根据已知条件,可以求得两组同学数学成绩的平均分都为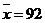 .……………………………3分
.……………………………3分
所以乙组四名同学数学成绩的方差为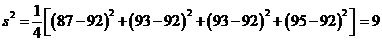 .
.
…………5分
(3)解:分别从甲、乙两组同学中各随机选取一名同学,共有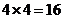 种可能的结果.……………6分
种可能的结果.……………6分
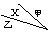 这两名同学成绩之差的绝对值
这两名同学成绩之差的绝对值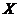 的所有情况如下表:
的所有情况如下表:
|
|
87 |
89 |
96 |
96 |
|
87 |
0 |
2 |
9 |
9 |
|
93 |
6 |
4 |
3 |
3 |
|
93 |
6 |
4 |
3 |
3 |
|
95 |
8 |
6 |
1 |
1 |
所以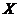 的所有可能取值为0,1,2,3,4,6,8,9.…………………………………………………8分
的所有可能取值为0,1,2,3,4,6,8,9.…………………………………………………8分
由表可得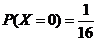 ,
,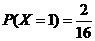 ,
,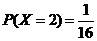 ,
,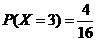 ,
,
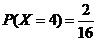 ,
,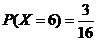 ,
,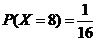 ,
,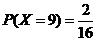 .
.
所以随机变量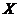 的分布列为:
的分布列为:
|
|
0 |
1 |
2 |
3 |
4 |
6 |
8 |
|
||
|
|
|
|
|
|
|
|
|
|
随机变量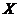 的数学期望为
的数学期望为

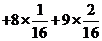 ………11分
………11分
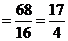 .……………………………………………………………12分
.……………………………………………………………12分


 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案科目:高中数学 来源:2013届山西大学附中高二第二学期5月月考数学试卷(解析版) 题型:选择题
某赛季,甲、乙两名篮球运动员都参加了7场比赛,他们所有比赛
得分的情况用如图1所示的茎叶图表示,则甲、乙两名运动员得分
的平均数分别为( )
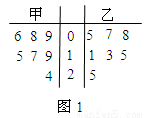
A.14、12 B.13、12
C.14、13 D.12、14
查看答案和解析>>
科目:高中数学 来源:2011-2012学年广东省广州市高三综合测试(一)理科数学试卷(解析版) 题型:解答题
.(本小题满分12分)
如图4所示的茎叶图记录了甲、乙两个小组(每小组4人)在期末考试中
的数学成绩.乙组记录中有一个数据模糊,无法确认,在图中以 表示.
表示.
已知甲、乙两个小组的数学成绩的平均分相同.
(1)求 的值;
的值;
(2)求乙组四名同学数学成绩的方差;
(3)分别从甲、乙两组同学中各随机选取一名同学,记这两名同学数学
成绩之差的绝对值为 ,求随机变量
,求随机变量 的分布列和均值(数学期望).
的分布列和均值(数学期望).

查看答案和解析>>
科目:高中数学 来源:2011年浙江省高一上学期期末考试数学试卷 题型:填空题
Ⅱ.填空题(共6题,每小题4分;满分24分),
11. 在如图3所示的茎叶图中,若中间一列的数字表示十位数,
两边的数字表示个位数,则甲组数据的中位数是 ,
乙组数据的平均数是 .

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com