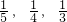练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    某同学参加北大、清华、科大三所学校的自主命题招生考试，其被录取的概率分别为数学公式（各学校是否录取他相互独立，允许他可以被多个学校同时录取）．
    （1）求此同学没有被任何学校录取的概率；
    （2）求此同学至少被两所学校录取的概率．

    解：（1）该同学被北大，清华，科大录取分别记为事件A，B，C，
    则该同学没有被任何学校录取记为事件D，且．…（2分）
    又∵是相互独立的，…（3分）
    ∴=．…（6分）
    （2）设此同学至少被两所学校录取记为事件E，则．…（9分）
    ∴=
    =．…（12分）
    分析：（1）该同学被北大，清华，科大录取分别记为事件A，B，C，则该同学没有被任何学校录取记为事件D，则由，运算求得结果．
    （2）设此同学至少被两所学校录取记为事件E，再根据 ，运算求得结果．
    点评：本题主要考查相互独立事件的概率乘法公式的应用，体现了分类讨论的数学思想，属于基础题．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    某同学参加北大、清华、科大三所学校的自主命题招生考试，其被录取的概率分别为
    1
    5
    ，
    1
    4
    ，
    1
    3
    （各学校是否录取他相互独立，允许他可以被多个学校同时录取）．
    （1）求此同学没有被任何学校录取的概率；
    （2）求此同学至少被两所学校录取的概率．

    查看答案和解析>>

    科目：高中数学 来源：2014届江西省高二下学期第二次月考文科数学试卷（解析版） 题型：填空题

    某同学参加北大、清华、科大三所学校的自主命题招生考试，其被录取的概率分别为（各学校是否录取他相互独立，允许他可以被多个学校同时录取）.则此同学至少被两所学校录取的概率为_____.

     

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

    某同学参加北大、清华、科大三所学校的自主命题招生考试，其被录取的概率分别为
    1
    5
    ，
    1
    4
    ，
    1
    3
    （各学校是否录取他相互独立，允许他可以被多个学校同时录取）．
    （1）求此同学没有被任何学校录取的概率；
    （2）求此同学至少被两所学校录取的概率．

    查看答案和解析>>

    科目：高中数学 来源：2013届安徽省宿州市高二下学期期中质量检测文科数学试卷（解析版） 题型：解答题

    某同学参加北大、清华、科大三所学校的自主命题招生考试，其被录取的概率分别为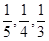（各学校是否录取他相互独立，允许他可以被多个学校同时录取）.

    （Ⅰ）求此同学没有被任何学校录取的概率；

    （Ⅱ）求此同学至少被两所学校录取的概率.

    【解析】本试题主要考查了独立事件的概率乘法公式的运用，以及运用对立事件求解概率的方法的综合运用。

     

    查看答案和解析>>

    同步练习册答案