
【题目】若二次函数f(x)满足f(x+1)﹣f(x)=4x+6,且f(0)=3.
(Ⅰ)求f(x)的解析式;
(Ⅱ)设g(x)=f(x)+(a﹣2)x2+(2a+2)x,g(x)在[﹣2,+∞)单调递增,求a的取值范围.
【答案】(Ⅰ)f(x)=2x2+4x+3;(Ⅱ)[0,3]
【解析】
(I)采用待定系数法即可求解;
(II)先将![]() 表达式化简,得
表达式化简,得![]() ,再对参数
,再对参数![]() 进行分类讨论,分为一次函数和二次函数两种情况求解,当函数为二次函数时,结合开口和对称轴的关系判断即可
进行分类讨论,分为一次函数和二次函数两种情况求解,当函数为二次函数时,结合开口和对称轴的关系判断即可
(I)设f(x)=ax2+bx+c,(a≠0),∵f(x+1)﹣f(x)=4x+6,且f(0)=3,
∴a(x+1)2+b(x+1)+c﹣(ax2+bx+c)=4x+6,且c=3,整理可得,2ax+a+b=4x+6,
∴2a=4,a+b=6,c=3,∴a=2,b=4,c=3,∴f(x)=2x2+4x+3;
(II)由(Ⅰ)可知,g(x)=f(x)+(a﹣2)x2+(2a+2)x=ax2+(2a+6)x+3,
当a=0时,g(x)=6x+3在[﹣2,+∞)单调递增,符合题意,
当a≠0时,对称轴x![]() ,由g(x)在[﹣2,+∞)单调递增可得,
,由g(x)在[﹣2,+∞)单调递增可得,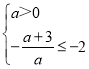 ,解可得,0<a≤3,
,解可得,0<a≤3,
综上可得,a的范围[0,3].


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】称正整数集合 A={a1,a2,…,an}(1≤a1<a2<…<an,n≥2)具有性质 P:如果对任意的i,j(1≤i≤j≤n),![]() 与
与![]() 两数中至少有一个属于A.
两数中至少有一个属于A.
(1)分别判断集合{1,3,6}与{1,3,4,12}是否具有性质 P;
(2)设正整数集合 A={a1,a2,…,an}(1≤a1<a2<…<an,n≥2)具有性质 P.证明:对任意1≤i≤n(i∈N*),ai都是an的因数;
(3)求an=30时n的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,抛物线
中,抛物线![]() ,三点
,三点![]() ,
,![]() ,
,![]() 中仅有一个点在抛物线
中仅有一个点在抛物线![]() 上.
上.
(Ⅰ)求![]() 的方程;
的方程;
(Ⅱ)设直线![]() 不经过
不经过![]() 点且与
点且与![]() 相交于
相交于![]() 两点.若直线
两点.若直线![]() 与
与![]() 的斜率之和为
的斜率之和为![]() ,证明:
,证明:![]() 过定点.
过定点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着电商的快速发展,快递业突飞猛进,到目前,中国拥有世界上最大的快递市场.某快递公司收取快递费用的标准是:重量不超过![]() 的包裹收费10元;重量超过
的包裹收费10元;重量超过![]() 的包裹,除
的包裹,除![]() 收费10元之外,每超过
收费10元之外,每超过![]() (不足
(不足![]() ,按
,按![]() 计算)需再收5元.
计算)需再收5元.
该公司将最近承揽的100件包裹的重量统计如下:
包裹重量(单位: | 1 | 2 | 3 | 4 | 5 |
包裹件数 | 43 | 30 | 15 | 8 | 4 |
公司对近60天,每天揽件数量统计如下表:
包裹件数范围 | 0~100 | 101~200 | 201~300 | 301~400 | 401~500 |
包裹件数(近似处理) | 50 | 150 | 250 | 350 | 450 |
天数 | 6 | 6 | 30 | 12 | 6 |
以上数据已做近似处理,并将频率视为概率.
(1)计算该公司未来5天内恰有2天揽件数在101~300之间的概率;
(2)①估计该公司对每件包裹收取的快递费的平均值;
②根据以往的经验,公司将快递费的三分之一作为前台工作人员的工资和公司利润,剩余的用作其他费用.目前前台有工作人员3人,每人每件揽件不超过150件,日工资100元.公司正在考虑是否将前台工作人员裁减1人,试计算裁员前后公司每日利润的数学期望,若你是公司老总,是否进行裁减工作人员1人?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市统计局就某地居民的月收入调查了10000人,并根据所得数据画出样本的频率分布直方图,每个分组包括左端点,不包括右端点,如第一组表示收入在![]() .
.
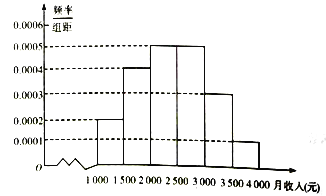
(1)求居民收入在![]() 的频率;
的频率;
(2)根据频率分布直方图算出样本数据的中位数、平均数及其众数;
(3)为了分析居民的收入与年龄、职业等方面的关系,从这10000人中用分层抽样方法抽出100人作进一步分析,则应月收入为![]() 的人中抽取多少人?
的人中抽取多少人?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校在九年级上学期开始时要掌握全年级学生每分钟跳绳的情况,随机抽取了100名学生进行测试,得到频率分布直方图(如图),且规定计分规则如下表:
每分钟跳绳个数 |
|
|
|
|
得分 | 17 | 18 | 19 | 20 |

(1)请估计学生的跳绳个数的众数和平均数(保留整数);
(2)若从跳绳个数在![]() ,
,![]() 两组中按分层抽样的方法抽取9人参加正式测试,并从中任意选取2人,求2人得分之和不大于34分的概率.
两组中按分层抽样的方法抽取9人参加正式测试,并从中任意选取2人,求2人得分之和不大于34分的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【2018河北保定市上学期期末调研】已知点![]() 到点
到点![]() 的距离比到
的距离比到![]() 轴的距离大1.
轴的距离大1.
(I)求点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(II)设直线![]() :
: ![]() ,交轨迹
,交轨迹![]() 于
于![]() 、
、![]() 两点,
两点, ![]() 为坐标原点,试在轨迹
为坐标原点,试在轨迹![]() 的
的![]() 部分上求一点
部分上求一点![]() ,使得
,使得![]() 的面积最大,并求其最大值.
的面积最大,并求其最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面四边形ABCD中, AB=2,BD=![]() ,AB⊥BC,∠BCD=2∠ABD,△ABD的面积为2.
,AB⊥BC,∠BCD=2∠ABD,△ABD的面积为2.

(1)求AD的长;
(2)求△CBD的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com