分析:(I)取BC中点O,连接AO. 可由面面垂直的性质得到AO⊥平面B
1C
1CB,令B
1C
1中点为O
1,以0为原点,OB,OO
1,OA的方向为x,y,z轴的正方向建立空间直角坐标系,分别求出向量
,
,
的坐标,用向量法可得
⊥
,
⊥
,进而由线面垂直的判定定理得到AB
1⊥平面A
1BD;
(II)求出平面AA
1D的法向量
,结合(I)中结论
为平面A
1BD的法向量,代入向量夹角公式,可得二面角A-A
1D-B的余弦值;
(Ⅲ)由(I)中
为平面A
1BD的法向量,求出向量
的坐标,代入
d=,可得点C到平面A
1BD的距离.
解答: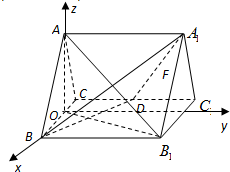
解:(I)取BC中点O,连接AO.
∴△ABC为正三角形,
∴AO⊥BC.
∵在正三棱柱ABC-A
1B
1C
1中,平面ABC⊥平面B
1C
1CB,
∴AO⊥平面B
1C
1CB,
取B
1C
1中点O
1,以0为原点,OB,OO
1,OA的方向为x,y,z轴的正方向建立空间直角坐标系,
则B(1,0,0),D(-1,1,0),A
1(0,2,
),A(0,0,
),B
1(1,2,0),
∴
=(1,2,-
),
=(-2,1,0),
=(-1,2,
).
∵
•
=-2+2=0,
•
=-1+4-3=0
∴
⊥
,
⊥
∴AB
1⊥平面A
1BD;
(Ⅱ)设平面AA
1D的法向量为
=(x,y,z).
∵
=(-1,1,-
),
=(0,2,0).
⊥
,
⊥
,
∴
,即
令z=1得
=(
-,0,1)
由(I)知AB
1⊥平面A
1BD,
∴
为平面A
1BD的法向量.
∴
cos<,>==-∴二面角A-A
1D-B的余弦值为
.
(3)由(2),
为平面A
1BD的法向量,
又∵
=(-2,0,0),
=(1,2,-
),.
∴点C到平面A
1BD的距离
d===.
点评:本题考查的知识点是二面角的平面角及其求法,直线与平面垂直的判定,点到平面的距离,其中建立空间坐标系,将空间线面关系,夹角问题转化为向量问题是解答的关键.

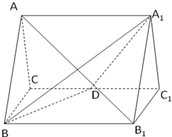 如图,三棱柱ABC-A1B1C1的所有棱长都为2,D为CC1中点,BB1⊥平面ABC
如图,三棱柱ABC-A1B1C1的所有棱长都为2,D为CC1中点,BB1⊥平面ABC 解:(I)取BC中点O,连接AO.
解:(I)取BC中点O,连接AO. 

 如图,三棱柱ABC-A1B1C1中,AA1⊥平面ABC,AB⊥AC,D、E分别为AA1、B1C的中点,AB=AC.
如图,三棱柱ABC-A1B1C1中,AA1⊥平面ABC,AB⊥AC,D、E分别为AA1、B1C的中点,AB=AC. (2012•黑龙江)如图,三棱柱ABC-A1B1C1中,侧棱垂直底面,∠ACB=90°,AC=BC=
(2012•黑龙江)如图,三棱柱ABC-A1B1C1中,侧棱垂直底面,∠ACB=90°,AC=BC= 如图,三棱柱ABC-A1B1C1的底面ABC为正三角形,侧棱AA1⊥平面ABC,D是BC中点,且AA1=AB
如图,三棱柱ABC-A1B1C1的底面ABC为正三角形,侧棱AA1⊥平面ABC,D是BC中点,且AA1=AB (2012•大连二模)如图,三棱柱ABC-A′B′C′,cc′=
(2012•大连二模)如图,三棱柱ABC-A′B′C′,cc′=