对于函数f(x)=a x2+(b+1)x+b-2(a≠0),若存在实数 x0,使f( x0)=x0成立,则称 x0为f(x)的不动点
(1)当a=2,b=-2时,求f(x)的不动点;
(2)若对于任何实数b,函数f(x)恒有两个相异的不动点,求实数a的取值范围;
(3)在(2)的条件下判断直线L:y=ax+1与圆(x-2)2+(y+2)2=4 a2+4的位置关系.
解:(1)f(x)=a x
2+(b+1)x+b-2(a≠0),
当a=2,b=-2时,f(x)=2 x
2-x-4,
设x为其不动点,即2 x
2-x-4=x
则2 x
2-2x-4=0,解得 x
1=-1,x
2=2
即f(x)的不动点为-1,2…..(4分)
(2)由f(x)=x得a x
2+bx+b-2=0
关于x的方程有相异实根,则 b
2-4a(b-2)>0,即 b
2-4ab+8a>0
又对所有的b∈R,b
2-4ab+8a>0恒成立
故有(4a)
2-4•8a<0,得0<a<2….(10分)
(3)由圆的方程得圆心M(2,-2),半径
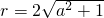
M到直线y=ax+1的距离
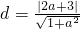
比较d与r的大小:
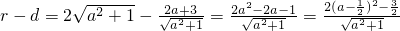
…..(9分)
当
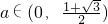
时,r<d,直线与圆相离;
当
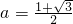
时,r=d,直线与圆相切;
当
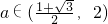
时,r>d,直线与圆相交(16分).
分析:(1)当a=2,b=-2时,f(x)=2x
2-x-4,设x为其不动点,即2x
2-x-4=x解之即可求出所求;
(2)由f(x)=x得a x
2+bx+b-2=0,关于x的方程有相异实根,则 b
2-4a(b-2)>0,对所有的b∈R,b
2-4ab+8a>0恒成立,根据判别式即可求出a的范围;
(3)由圆的方程得圆心M(2,-2),求出半径和M到直线y=ax+1的距离d,比较d与r的大小,讨论a的范围可得直线与圆的位置关系.
点评:本题互异考查了新定义,以及恒成立问题和直线与圆的位置关系的判定,属于中档题.

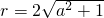
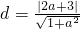
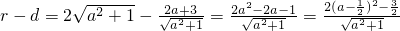 …..(9分)
…..(9分)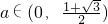 时,r<d,直线与圆相离;
时,r<d,直线与圆相离;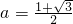 时,r=d,直线与圆相切;
时,r=d,直线与圆相切;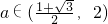 时,r>d,直线与圆相交(16分).
时,r>d,直线与圆相交(16分).
