【答案】
分析:(1)利用二项展开式的通项公式求出倒数第三项的系数列出方程求出n;
利用二项展开式的通项公式求出通项,令x的指数为3求出展开式含x
3的项.
(2)由通项得到项的系数与二项式系数相等,据二项式系数的性质:展开式中间项的二项式系数最大求出系数最大的项.
解答:解:(1)由题设知C
nn-2=45,即C
n2=45,
∴n=10.
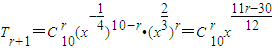
,
令
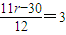
,得r=6,
含x
3的项为T
7=C
106x
3=C
104x
3=210x
3.
(2)由通项知,展开式项的系数是二项式系数
据二项式系数的性质:展开式中间项的二项式系数最大
故系数最大的项为中间项,即
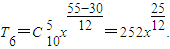 点评:
点评:本题考查利用二项展开式的通项公式解决二项展开式的特定项问题;二项式系数的性质:展开式中间项的二项式系数最大.

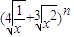 展开式中的倒数第三项的系数为45,求:
展开式中的倒数第三项的系数为45,求: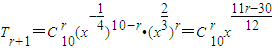 ,
,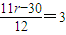 ,得r=6,
,得r=6,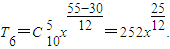


 阶梯计算系列答案
阶梯计算系列答案