
【题目】若![]() 、
、![]() 是异面直线,则下列命题中的假命题为( )
是异面直线,则下列命题中的假命题为( )
A.过直线![]() 可以作一个平面并且只可以作一个平面
可以作一个平面并且只可以作一个平面![]() 与直线
与直线![]() 平行
平行
B.过直线![]() 至多可以作一个平面
至多可以作一个平面![]() 与直线
与直线![]() 垂直
垂直
C.唯一存在一个平面![]() 与直线
与直线![]() 、
、![]() 等距
等距
D.可能存在平面![]() 与直线
与直线![]() 、
、![]() 都垂直
都垂直
【答案】D
【解析】
在A中,把直线![]() 平移与直线
平移与直线![]() 相交,确定一个平面内平行于
相交,确定一个平面内平行于![]() ;在B中,反设过直线
;在B中,反设过直线![]() 能作平面
能作平面![]() 、
、![]() 使得
使得![]() 、
、![]() ,推出矛盾;在C中,过异面直线
,推出矛盾;在C中,过异面直线![]() 、
、![]() 的公垂线段的中点作与该公垂线垂直的平面可满足条件;在D中,若存在平面
的公垂线段的中点作与该公垂线垂直的平面可满足条件;在D中,若存在平面![]() 与直线
与直线![]() 、
、![]() 都垂直,则
都垂直,则![]() .
.
在A中,由于![]() 、
、![]() 是异面直线,把直线
是异面直线,把直线![]() 平移与直线
平移与直线![]() 相交,可确定一个平面,这个平面与直线
相交,可确定一个平面,这个平面与直线![]() 平行,A选项正确;
平行,A选项正确;
在B中,若过直线![]() 能作平面
能作平面![]() 、
、![]() 使得
使得![]() 、
、![]() ,则
,则![]() ,这与
,这与![]() 矛盾,
矛盾,
所以,过直线![]() 最多只能作一个平面
最多只能作一个平面![]() 与直线
与直线![]() 垂直,由
垂直,由![]() ,可得
,可得![]() ,
,
当直线![]() 与
与![]() 不垂直时,过直线
不垂直时,过直线![]() 不能作平面与直线
不能作平面与直线![]() 垂直,B选项正确;
垂直,B选项正确;
在C中,由于![]() 、
、![]() 是异面直线,则两直线的公垂线段只有一条,过该公垂线段的中点作平面
是异面直线,则两直线的公垂线段只有一条,过该公垂线段的中点作平面![]() 与该公垂线垂直,这样的平面
与该公垂线垂直,这样的平面![]() 有且只有一个,且这个平面
有且只有一个,且这个平面![]() 与直线
与直线![]() 、
、![]() 等距,C选项正确;
等距,C选项正确;
在D中,若存在平面![]() 与直线
与直线![]() 、
、![]() 都垂直,由直线与平面垂直的性质定理可得
都垂直,由直线与平面垂直的性质定理可得![]() ,D错误.
,D错误.
故选:D.


 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案科目:高中数学 来源: 题型:
【题目】已知![]() ,
,![]() ,
,![]() ,
,![]() 是各项均为正数的等差数列,其公差
是各项均为正数的等差数列,其公差![]() 大于零.若线段
大于零.若线段![]() ,
,![]() ,
,![]() ,
,![]() 的长分别为
的长分别为![]() ,
,![]() ,
,![]() ,
,![]() ,则( ).
,则( ).
A.对任意的![]() ,均存在以
,均存在以![]() ,
,![]() ,
,![]() 为三边的三角形
为三边的三角形
B.对任意的![]() ,均不存在以
,均不存在以![]() ,
,![]() ,
,![]() 为三边的三角形
为三边的三角形
C.对任意的![]() ,均存在以
,均存在以![]() ,
,![]() ,
,![]() 为三边的三角形
为三边的三角形
D.对任意的![]() ,均不存在以
,均不存在以![]() ,
,![]() ,
,![]() 为三边的三角形
为三边的三角形
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
,![]() ,直线l与椭圆C交于P,Q两点,且点M满足
,直线l与椭圆C交于P,Q两点,且点M满足![]() .
.
(1)若点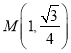 ,求直线
,求直线![]() 的方程;
的方程;
(2)若直线l过点![]() 且不与x轴重合,过点M作垂直于l的直线
且不与x轴重合,过点M作垂直于l的直线![]() 与y轴交于点
与y轴交于点![]() ,求实数t的取值范围.
,求实数t的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (
(![]() 为常数,
为常数,![]() 且
且![]() ),且数列
),且数列![]() 是首项为
是首项为![]() ,公差为
,公差为![]() 的等差数列.
的等差数列.
(1)求证:数列![]() 是等比数列;
是等比数列;
(2)若![]() ,当
,当![]() 时,求数列
时,求数列![]() 的前
的前![]() 项和
项和![]() 的最小值;
的最小值;
(3)若![]() ,问是否存在实数
,问是否存在实数![]() ,使得
,使得![]() 是递增数列?若存在,求出
是递增数列?若存在,求出![]() 的范围;若不存在,说明理由.
的范围;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两位同学参加诗词大赛,各答3道题,每人答对每道题的概率均为![]() ,且各人是否答对每道题互不影响.
,且各人是否答对每道题互不影响.
(Ⅰ)用![]() 表示甲同学答对题目的个数,求随机变量
表示甲同学答对题目的个数,求随机变量![]() 的分布列和数学期望;
的分布列和数学期望;
(Ⅱ)设![]() 为事件“甲比乙答对题目数恰好多2”,求事件
为事件“甲比乙答对题目数恰好多2”,求事件![]() 发生的概率.
发生的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示:湖面上甲、乙、丙三艘船沿着同一条直线航行,某一时刻,甲船在最前面的![]() 点处,乙船在中间
点处,乙船在中间![]() 点处,丙船在最后面的
点处,丙船在最后面的![]() 点处,且
点处,且![]() .一架无人机在空中的
.一架无人机在空中的![]() 点处对它们进行数据测量,在同一时刻测得
点处对它们进行数据测量,在同一时刻测得![]() ,
, ![]() .(船只与无人机的大小及其它因素忽略不计)
.(船只与无人机的大小及其它因素忽略不计)

(1)求此时无人机到甲、丙两船的距离之比;
(2)若此时甲、乙两船相距100米,求无人机到丙船的距离.(精确到1米)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com