
【题目】函数y=sin(2x+φ)的图象沿x轴向左平移 ![]() 个单位后,得到一个偶函数的图象,则φ的一个可能的值为( )
个单位后,得到一个偶函数的图象,则φ的一个可能的值为( )
A.![]()
B.![]()
C.0
D.![]()
【答案】B
【解析】解:令y=f(x)=sin(2x+φ),
则f(x+ ![]() )=sin[2(x+
)=sin[2(x+ ![]() )+φ]=sin(2x+
)+φ]=sin(2x+ ![]() +φ),
+φ),
∵f(x+ ![]() )为偶函数,
)为偶函数,
∴ ![]() +φ=kπ+
+φ=kπ+ ![]() ,
,
∴φ=kπ+ ![]() ,k∈Z,
,k∈Z,
∴当k=0时,φ= ![]() .
.
故φ的一个可能的值为 ![]() .
.
故选B.
【考点精析】根据题目的已知条件,利用函数y=Asin(ωx+φ)的图象变换的相关知识可以得到问题的答案,需要掌握图象上所有点向左(右)平移![]() 个单位长度,得到函数
个单位长度,得到函数![]() 的图象;再将函数
的图象;再将函数![]() 的图象上所有点的横坐标伸长(缩短)到原来的
的图象上所有点的横坐标伸长(缩短)到原来的![]() 倍(纵坐标不变),得到函数
倍(纵坐标不变),得到函数![]() 的图象;再将函数
的图象;再将函数![]() 的图象上所有点的纵坐标伸长(缩短)到原来的
的图象上所有点的纵坐标伸长(缩短)到原来的![]() 倍(横坐标不变),得到函数
倍(横坐标不变),得到函数![]() 的图象.
的图象.


 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案科目:高中数学 来源: 题型:
【题目】已知数列{an}满足a1= ![]() ,an+1=10an+1.
,an+1=10an+1.
(1)证明数列{an+ ![]() }是等比数列,并求数列{an}的通项公式;
}是等比数列,并求数列{an}的通项公式;
(2)数列{bn}满足bn=lg(an+ ![]() ),Tn为数列{
),Tn为数列{ ![]() }的前n项和,求证:Tn<
}的前n项和,求证:Tn< ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国是世界上严重缺水的国家,某市政府为了鼓励居民节约用水,计划调整居民生活用水收费方案,拟确定一个合理的月用水量标准x(吨),一位居民的月用水量不超过x的部分按平价收费,超过x的部分按议价收费.为了了解居民用水情况,通过抽样,获得了某年100位居民每人的月均用水量(单位:吨),将数据按照[0,0.5),[0.5,1),…,[4,4.5)分成9组,制成了如图所示的频率分布直方图.
(Ⅰ)求直方图中a的值;
(Ⅱ)若将频率视为概率,从该城市居民中随机抽取3人,记这3人中月均用水量不低于3吨的人数为X,求X的分布列与数学期望.
(Ⅲ)若该市政府希望使85%的居民每月的用水量不超过标准x(吨),估计x的值(精确到0.01),并说明理由.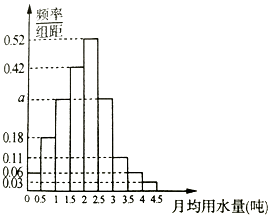
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】知 ![]() =(2λsinx,sinx+cosx),
=(2λsinx,sinx+cosx), ![]() =(
=( ![]() cosx,λ(sinx﹣cosx))(λ>0),函数f(x)=
cosx,λ(sinx﹣cosx))(λ>0),函数f(x)= ![]()
![]() 的最大值为2.
的最大值为2.
(1)求函数f(x)的单调递减区间;
(2)在△ABC中,内角A,B,C的对边分别为a,b,c,cosA= ![]() ,若f(A)﹣m>0恒成立,求实数m的取值范围.
,若f(A)﹣m>0恒成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点P在圆C:x2+y2=4上,而Q为P在x轴上的投影,且点N满足 ![]() ,设动点N的轨迹为曲线E.
,设动点N的轨迹为曲线E.
(1)求曲线E的方程;
(2)若A,B是曲线E上两点,且|AB|=2,O为坐标原点,求△AOB的面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥P﹣ABCD的底面ABCD是正方形,PD⊥平面ABCD,E为PB上的点,且2BE=EP. 
(1)证明:AC⊥DE;
(2)若PC= ![]() BC,求二面角E﹣AC﹣P的余弦值.
BC,求二面角E﹣AC﹣P的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将一颗骰子投掷两次,第一次出现的点数记为a,第二次出现的点数记为b,设两条直线l1:ax+by=2与l2:x+2y=2平行的概率为P1 , 相交的概率为P2 , 则点P(36P1 , 36P2)与圆C:x2+y2=1098的位置关系是( )
A.点P在圆C上
B.点P在圆C外
C.点P在圆C内
D.不能确定
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在正方体ABCD﹣A1B1C1D1中,E、F分别为棱BB1、BC的中点,则异面直线AB1与EF所成角的大小为( )
A.30°
B.45°
C.60°
D.90°
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知三棱锥P﹣ABC的底面是等腰直角三角形,且∠ACB= ![]() ,侧面PAB⊥底面ABC,AB=PA=PB=2.则这个三棱锥的三视图中标注的尺寸x,y,z分别是( )
,侧面PAB⊥底面ABC,AB=PA=PB=2.则这个三棱锥的三视图中标注的尺寸x,y,z分别是( ) 
A.![]() ,1,
,1, ![]()
B.![]() ,1,1
,1,1
C.2,1, ![]()
D.2,1,1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com