Question

【题目】某地区有100名学员参加交通法规考试，考试成绩的频率分布直方图如图所示．其中成绩分组区间是：第1组：[75，80），第2组：[80，85），第3组：[85，90），第4组：[90，95），第5组：[95，100]．
（1）求图中a的值，并估计此次考试成绩的中位数（结果保留一位小数）；
（2）在第2、4小组中用分层抽样的方法抽取5人，再从这5人中随机选取2人进行面试，求至少有一人来自第2小组的概率．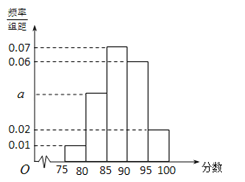

Answer 1

【答案】
解：（1）由（0.01+0.02+a+0.06+0.07）×5=1，
得：a=0.04，
设此次考试成绩中位数的估计值为x：则0.05+0.2+（x﹣85）×0.07=0.5，
得x≈88.6；
（2）由频率分布直方图知：第2、5小组中的人数分别为20，30，
∴从第2、4小组中抽取的人数分别为2，3，分别设为a，b和c，d，e，
这5人中随机选取2人所有基本事件为：（a，b），（a，c），（a，d），（a，e），（b，c），（b，d），（b，e），（c，d），
（c，e），（d，e）共10个，
其中至少有一个来自第2小组的基本事件为（a，b），（a，c），（a，d），（a，e），
（b，c），（b，d），（b，e） 共7个．
故至少有一人来自第2小组的概率p=。
【解析】（1）由频率和为1求得a值，然后再由中位数两边矩形的面积相等列式求得中位数的估计值；
（2）求出从第2、4小组中抽取的人数，枚举得到从5人中随机选取2人的所有基本事件数及其中至少有一个来自第2小组的基本事件，然后由古典概型概率计算公式得答案．
【考点精析】利用频率分布直方图对题目进行判断即可得到答案，需要熟知频率分布表和频率分布直方图，是对相同数据的两种不同表达方式.用紧凑的表格改变数据的排列方式和构成形式，可展示数据的分布情况.通过作图既可以从数据中提取信息，又可以利用图形传递信息．