
已知数列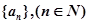 满足
满足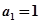 ,且对任意非负整数
,且对任意非负整数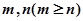 均有:
均有: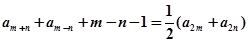 .
.
(1)求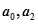 ;
;
(2)求证:数列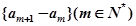 是等差数列,并求
是等差数列,并求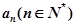 的通项;
的通项;
(3)令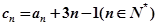 ,求证:
,求证: .
.
:(1)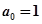 ,
,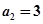 ;(2)
;(2)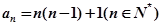 ;(3)详见解析.
;(3)详见解析.
【解析】
试题分析:(1)对m、n赋值,想方设法将条件变出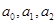 .为了得到
.为了得到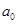 ,显然令m=n即可.
,显然令m=n即可.
为了得到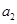 ,令m=1,n=0即可.
,令m=1,n=0即可.
(2)首先要想办法得相邻两项(三项也可)间的递推关系.
要证数列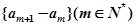 是等差数列,只需证明
是等差数列,只需证明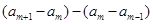 为常数即可.
为常数即可.
(3)数列中有关和的不等式的证明一般有以下两种方向,一是先求和后放缩,二是先放缩后求和.在本题中,易得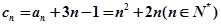 ,∴
,∴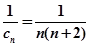
这是典型的用裂项法求和的题.故先求出和来,然后再用放缩法证明不等式.
试题解析:(1)令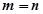 得
得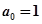 , 1分
, 1分
令 ,得
,得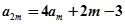 ,∴
,∴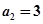 3分
3分
(2)令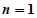 ,得:
,得: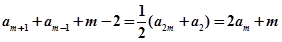
∴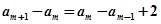 ,又
,又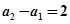 ,
,
∴数列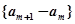 是以2为首项,2为公差的等差数列.
是以2为首项,2为公差的等差数列.
∴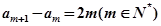
∴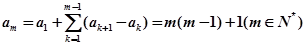
∴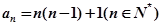 9分
9分
(3)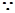
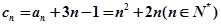 ∴
∴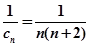
∴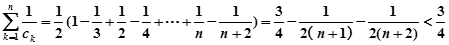 13分
13分
考点:1、递推数列;2、等差数列;3、不等式的证明.


 阅读快车系列答案
阅读快车系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com