
| 3 |
| 2 |
| 5 |
| 2 |
| π |
| 8 |
| 5π |
| 4 |
| π |
| 2 |
| π |
| 3 |
| π |
| 3 |
| 2 |
| π |
| 4 |
| 2 |
| 2 |
| 3 |
| 2 |
| 5π |
| 2 |
| π |
| 2 |
| 5π |
| 4 |
| 5π |
| 4 |
| π |
| 2 |
| 3π |
| 8 |
| kπ |
| 2 |
| π |
| 8 |
| π |
| 2 |
| π |
| 2 |
| π |
| 3 |
| π |
| 6 |
| π |
| 6 |


科目:高中数学 来源: 题型:
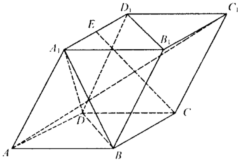 (2008•成都三模)已知平行六面体ABCD-A1B1C1D1中,∠A1AD=∠A1AB=∠BAD=60°,AA1=AB=AD,E为A1D1的中点.给出下列四个命题:①∠BCC1为异面直线AD与CC1所成的角;②三棱锥A1-ABD是正三棱锥;③CE⊥平面BB1D1D;④
(2008•成都三模)已知平行六面体ABCD-A1B1C1D1中,∠A1AD=∠A1AB=∠BAD=60°,AA1=AB=AD,E为A1D1的中点.给出下列四个命题:①∠BCC1为异面直线AD与CC1所成的角;②三棱锥A1-ABD是正三棱锥;③CE⊥平面BB1D1D;④| CE |
| 1 |
| 2 |
| AD |
| AB |
| AA1 |
查看答案和解析>>
科目:高中数学 来源: 题型:
①若直线l∥平面α,则直线l的垂线必平行于平面α;
②若直线l与平面α相交,则有且只有一个平面经过直线l与平面α垂直;
③若一个三棱锥每两个相邻侧面所成的角都相等,则这个三棱锥是正三棱锥;
④若四棱柱的任意两条对角线相交且互相平分,则这个四棱柱为平行六面体.
其中,正确的命题是________________.(把你认为正确的命题的序号都填上)
查看答案和解析>>
科目:高中数学 来源:2014届四川省高二12月检测数学试卷(解析版) 题型:填空题
已知平行六面体ABCD-A1B1C1D1中,∠A1AD=∠A1AB=∠BAD=60°,AA1=AB=AD=1,E为A1D1的中点。

给出下列四个命题:①∠BCC1为异面直线 与CC1所成的角;②三棱锥A1-ABD是正三棱锥;③CE⊥平面BB1D1D;④
与CC1所成的角;②三棱锥A1-ABD是正三棱锥;③CE⊥平面BB1D1D;④ ;⑤|
;⑤| |=
|= .其中正确的命题有_____________.(写出所有正确命题的序号)
.其中正确的命题有_____________.(写出所有正确命题的序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
①正四棱柱一定是直平行六面体;
②四面体ABCD中,若点A在面BCD上的射影是△BCD的垂心,则点B在面ACD上的射影也是△ACD的垂心;
③经过球面上不同两点的球的小圆可能不存在.
其中假命题的个数为
A.0 B.1 C.2 D.3
查看答案和解析>>
科目:高中数学 来源:2008年四川省成都市高考数学三模试卷(文科)(解析版) 题型:解答题
 .其中正确的命题有 .(写出所有正确命题的序号)
.其中正确的命题有 .(写出所有正确命题的序号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com