
【题目】若y=|3sin(ωx+ ![]() )+2|的图象向右平移
)+2|的图象向右平移 ![]() 个单位后与自身重合,且y=tanωx的一个对称中心为(
个单位后与自身重合,且y=tanωx的一个对称中心为( ![]() ,0),则ω的最小正值为 .
,0),则ω的最小正值为 .
【答案】24
【解析】解:∵y=|3sin(ωx+ ![]() )+2|的图象向右平移
)+2|的图象向右平移 ![]() 个单位后与自身重合,
个单位后与自身重合,
∴ ![]() =k
=k ![]() ,k∈N,
,k∈N,
则ω=6k,k∈N,①
∵y=tanx的对称中心为( ![]() ,0),
,0),
∴y=tanωx(ω∈N*)的对称中心是( ![]() ,0),
,0),
又( ![]() ,0)是函数y=tanωx(ω∈N*)的一个对称中心,
,0)是函数y=tanωx(ω∈N*)的一个对称中心,
∴ ![]() =
= ![]() (k∈Z),
(k∈Z),
∴ω=24k,k∈N,②
由①②知,ω的最小正值为24.
故答案是:24.
【考点精析】利用函数y=Asin(ωx+φ)的图象变换对题目进行判断即可得到答案,需要熟知图象上所有点向左(右)平移![]() 个单位长度,得到函数
个单位长度,得到函数![]() 的图象;再将函数
的图象;再将函数![]() 的图象上所有点的横坐标伸长(缩短)到原来的
的图象上所有点的横坐标伸长(缩短)到原来的![]() 倍(纵坐标不变),得到函数
倍(纵坐标不变),得到函数![]() 的图象;再将函数
的图象;再将函数![]() 的图象上所有点的纵坐标伸长(缩短)到原来的
的图象上所有点的纵坐标伸长(缩短)到原来的![]() 倍(横坐标不变),得到函数
倍(横坐标不变),得到函数![]() 的图象.
的图象.


科目:高中数学 来源: 题型:
【题目】已知 ![]() 为等差数列,公差
为等差数列,公差 ![]() (
( ![]() ),且
),且![]() (
( ![]() )
)
(1)求证:当 ![]() 取不同自然数时,此方程有公共根;
取不同自然数时,此方程有公共根;
(2)若方程不同的根依次为![]() ,
, ![]() ,
, ![]() , …,
, …,![]() , …,求证:数列
, …,求证:数列 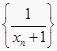 为等差数列。
为等差数列。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在下列命题中,下列选项正确的是( )
A. 在回归直线![]() 中,变量
中,变量![]() 时,变量
时,变量![]() 的值一定是15.
的值一定是15.
B. 两个变量相关性越强,则相关系数![]() 就越接近于1.
就越接近于1.
C. 在残差图中,残差点比较均匀落在水平的带状区域中即可说明选用的模型比较合适,与带状区域的宽度无关.
D. 若![]() 是两个相等的非零实数,则
是两个相等的非零实数,则![]() 是纯虚数.
是纯虚数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】奇函数f(x)定义域是(﹣1,0)∪(0,1),f(![]() )=0,当x>0时,总有(
)=0,当x>0时,总有(![]() x)f′(x)ln(1﹣x2)>2f(x)成立,则不等式f(x)>0的解集为( )
x)f′(x)ln(1﹣x2)>2f(x)成立,则不等式f(x)>0的解集为( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】据统计,仅在北京地区每天就有500万单快递等待派送,近5万多名快递员奔跑在一线,快递网点人员流动性也较强,各快递公司需要经常招聘快递员,保证业务的正常开展.下面是50天内甲、乙两家快递公司的快递员的每天送货单数统计表:
送货单数 | 30 | 40 | 50 | 60 | |
天数 | 甲 | 10 | 10 | 20 | 10 |
乙 | 5 | 15 | 25 | 5 | |
已知这两家快递公司的快递员的日工资方案分别为:甲公司规定底薪![]() 元,每单抽成
元,每单抽成![]() 元;乙公司规定底薪
元;乙公司规定底薪![]() 元,每日前
元,每日前![]() 单无抽成,超过
单无抽成,超过![]() 单的部分每单抽成
单的部分每单抽成![]() 元.
元.
(1)分别求甲、乙快递公司的快递员的日工资![]() (单位:元)与送货单数
(单位:元)与送货单数![]() 的函数关系式;
的函数关系式;
(2)若将频率视为概率,回答下列问题:
①记甲快递公司的快递员的日工资为![]() (单位:元),求
(单位:元),求![]() 的分布列和数学期望;
的分布列和数学期望;
②小赵拟到甲、乙两家快递公司中的一家应聘快递员的工作,如果仅从日收入的角度考虑,请你利用所学的统计学知识为他作出选择,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥PABC中,PA⊥底面ABCD,AD∥BC,AB=AD=AC=3,PA=BC=4,M为线段AD上一点,AM=2MD,N为PC的中点.

(Ⅰ)证明MN∥平面PAB;
(Ⅱ)求直线AN与平面PMN所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=x2﹣bx+alnx.
(1)若b=2,函数f(x)有两个极值点x1 , x2 , 且x1<x2 , 求实数a的取值范围;
(2)在(1)的条件下,证明:f(x2)>﹣ ![]() ;
;
(3)若对任意b∈[1,2],都存在x∈(1,e)(e为自然对数的底数),使得f(x)<0成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给定命题p:“若a2017>﹣1,则a>﹣1”;命题q:“x∈R,x2tanx2>0”,则下列命题中,真命题的是( )
A.p∨q
B.(¬p)∨q
C.(¬p)∧q
D.(¬p)∧(¬q)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com