Question

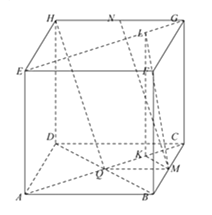
【题目】一个正方体的平面展开图及该正方体的直观图的示意图如图所示，在正方体中，设BC的中点为M，GH的中点为N

(1)请将字母F，G，H标记在正方体相应的顶点处（不需说明理由）；

(2)证明：直线MN∥平面BDH

（3）求异面直线MN与AG所成角的余弦值

Answer 1

【答案】（1）（2）见解析；（3）

【解析】

(1) 直接将平面图形折叠同时注意顶点的对应方式即可.(2)先证明QH∥MN，再证明MN∥平面BDH.(3)先证明就是异面直线AG与MN所成角（或其补角），再利用余弦定理求异面直线AG与MN所成角的余弦值为.

（1）直接将平面图形折叠同时注意顶点的对应方式即可，如图

(2)连接BD，取BD的中点Q，连接MQ，

因为M，Q为线段BC、BD中点，所以MQ∥CD∥GH且,

又因为N为GH中点，所以得到NH=MQ且NH∥MQ，

所以四边形QMNH为平行四边形，得到QH∥MN

又，所以MN∥平面BDH

(3)如图所示，在原正方体的右侧补上一个与其大小相等的正方体，连接GO，易得GO∥MN，就是异面直线AG与MN所成角（或其补角），

设正方体的棱长为2，则,

所以异面直线AG与MN所成角的余弦值为.