
【题目】在长方体ABCD﹣A1B1C1D1中,AB=BC=1,AA1=2,E为BB1中点. 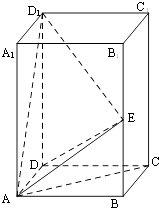
(1)证明:AC⊥D1E;
(2)求DE与平面AD1E所成角的正弦值.
【答案】
(1)证明:连接BD
∵ABCD﹣A1B1C1D1是长方体,
∴D1D⊥平面ABCD,
又AC平面ABCD
∴D1D⊥AC
在长方形ABCD中,AB=BC
∴BD⊥AC
又BD∩D1D=D
∴AC⊥平面BB1D1D,
而D1E平面BB1D1D
∴AC⊥D1E
(2)解:如图建立空间直角坐标系D﹣xyz,则A(1,0,0),D1(0,0,2),E(1,1,1),B(1,1,0), ![]()
设平面AD1E的法向量为 ![]() ,则
,则 ![]() ,
,
令z=1,则 ![]()
∴cos< ![]() ,
, ![]() >=
>= ![]() =
= ![]()
∴DE与平面AD1E所成角的正弦值为 ![]()

【解析】(1)根据已知中长方体ABCD﹣A1B1C1D1中,AB=BC=1,AA1=2,E是侧棱BB1的中点,结合长方体的几何特征,我们可得D1D⊥AC,BD⊥AC,结合线面垂直的判定定理即可得到AC⊥平面BB1D1D,即可得出结论;(2)建立空间直角坐标系,求出平面AD1E的法向量,利用向量的夹角公式,即可求DE与平面AD1E所成角的正弦值.
【考点精析】利用空间角的异面直线所成的角对题目进行判断即可得到答案,需要熟知已知![]() 为两异面直线,A,C与B,D分别是
为两异面直线,A,C与B,D分别是![]() 上的任意两点,
上的任意两点,![]() 所成的角为
所成的角为![]() ,则
,则 .
.


 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)当![]() 时,求
时,求![]() 的单调区间;
的单调区间;
(2)设![]() 是曲线
是曲线![]() 图象上的两个相异的点,若直线
图象上的两个相异的点,若直线![]() 的斜率
的斜率![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
(3)设函数![]() 有两个极值点
有两个极值点![]() 且
且![]() ,若
,若![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某科技公司生产一种手机加密芯片,其质量按测试指标划分为:指标大于或等于![]() 为合格品,小于
为合格品,小于![]() 为次品.现随机抽取这种芯片共
为次品.现随机抽取这种芯片共![]() 件进行检测,检测结果统计如表:
件进行检测,检测结果统计如表:
测试指标 |
|
|
|
|
|
芯片数量(件) |
|
|
|
|
|
已知生产一件芯片,若是合格品可盈利![]() 元,若是次品则亏损
元,若是次品则亏损![]() 元.
元.
(Ⅰ)试估计生产一件芯片为合格品的概率;并求生产![]() 件芯片所获得的利润不少于
件芯片所获得的利润不少于![]() 元的概率.
元的概率.
(Ⅱ)记![]() 为生产
为生产![]() 件芯片所得的总利润,求随机变量
件芯片所得的总利润,求随机变量![]() 的分布列和数学期望
的分布列和数学期望
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市共有初中学生270000人,其中初一年级,初二年级,初三年级学生人数分别为99000,90000,81000,为了解该市学生参加“开放性科学实验活动”的意向,现采用分层抽样的方法从中抽取一个容量为3000的样本,那么应该抽取初三年级的人数为( )
A.800
B.900
C.1000
D.1100
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在四棱锥![]() 中,
中, ![]() 平面
平面![]() 是
是![]() 的中点,
的中点, ![]() 是
是![]() 上的点且
上的点且![]() 为
为![]() 边
边![]() 上的高.
上的高.

(1)证明: ![]() 平面
平面![]() ;
;
(2)若![]() ,求三棱锥
,求三棱锥![]() 的体积;
的体积;
(3)在线段![]() 上是否存在这样一点
上是否存在这样一点![]() ,使得
,使得![]() 平面
平面![]() ?若存在,说出
?若存在,说出![]() 点的位置.
点的位置.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 是椭圆
是椭圆![]() 上关于原点
上关于原点![]() 对称的任意两点,且点
对称的任意两点,且点![]() 都不在
都不在![]() 轴上.
轴上.
(1)若![]() ,求证: 直线
,求证: 直线![]() 和
和![]() 的斜率之积为定值;
的斜率之积为定值;
(2)若椭圆长轴长为![]() ,点
,点![]() 在椭圆
在椭圆![]() 上,设
上,设![]() 是椭圆上异于点
是椭圆上异于点![]() 的任意两点,且
的任意两点,且![]() .问直线
.问直线![]() 是否过一个定点?若过定点,求出该定点坐标;若不过定点,请说明理由.
是否过一个定点?若过定点,求出该定点坐标;若不过定点,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com