Question

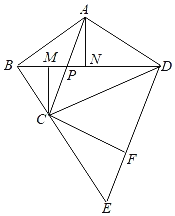
【题目】如图，平面四边形ABCD中，AC与BD交于点P，若3BP＝BD，AB＝ADBC，，则_____.

Answer 1

【答案】

【解析】

延长BC到E，使得BE＝3BC，连结DE，结合已知得3，由相似三角形性质得P是BD的三等分点，且AP＝PC，分别过A，C作BD的垂线，垂足为N，M，PM＝PN＝BM，得BC＝PC，过C作CF//AD交DE于F，则四边形ACFD是平行四边形，设BC＝1，计算出各线段长，可得CF⊥DE，四边形ACFD是矩形，这样可计算出，得所求比值．

延长BC到E，使得BE＝3BC，连结DE，

则3，又33，

∴3，

∴DE//AC，DE＝3AP.

∴，

∴，

∴P是BD的三等分点，且AP＝PC.

分别过A，C作BD的垂线，垂足为N，M， ∵，

∴PM＝PN＝BM，

∴BC＝PC，

过C作CF//AD交DE于F，则四边形ACFD是平行四边形，

设BC＝1，则AB＝AD，CE＝2BC＝2，CF＝AD，DE＝3PC＝3，

∴EFDE＝1，

∴CE2＝CF2+EF2，∴CF⊥DE，

∴四边形ACFD是矩形，∴∠CAD，

∴CD，

∴.

故答案为：.