Question

将直线y=0绕点（-1，0）顺时针旋转60°得到直线l，则直线l的方程是    ；直线l在y轴上的截距是    ．

Answer 1

【答案】分析：由题意可得直线l的倾斜角为120°，进而求得直线的斜率等于tan120°，用点斜式求直线方程，化为一般式，
根据截距的定义，求出直线l在y轴上的截距．
解答：解：直线y=0绕点（-1，0）顺时针旋转60°得到直线l，则直线l的倾斜角为120°，
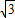
故直线的斜率等于tan120°=-，由点斜式求出直线的方程为 y-0=-（x+1），
即．
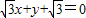
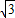
令x=0，可得y=-，故直线在y轴上的截距等于-．
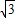
故答案为 ，-．
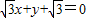
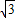
点评：本题主要考查直线的倾斜角和斜率的关系，用点斜式求直线方程，判断直线l的倾斜角为120°，是解题的关键，属于基础题．