
在![]() 中,内角A、B、C的对边长分别为
中,内角A、B、C的对边长分别为![]() 、
、![]() 、
、![]() ,已知
,已知![]() ,且
,且![]() 求b.
求b.![]()
![]()
分析:此题事实上比较简单,但考生反应不知从何入手.对已知条件(1)![]() 左侧是二次的右侧是一次的,学生总感觉用余弦定理不好处理,而对已知条件(2)
左侧是二次的右侧是一次的,学生总感觉用余弦定理不好处理,而对已知条件(2) ![]() 过多的关注两角和与差的正弦公式,甚至有的学生还想用现在已经不再考的积化和差,导致找不到突破口而失分.
过多的关注两角和与差的正弦公式,甚至有的学生还想用现在已经不再考的积化和差,导致找不到突破口而失分.
解法一:在![]() 中
中![]() 则由正弦定理及余弦定理有:
则由正弦定理及余弦定理有:![]() 化简并整理得:
化简并整理得:![]() .又由已知
.又由已知![]()
![]() .解得
.解得![]() .
.
解法二:由余弦定理得: ![]() .又
.又![]() ,
,![]() 。
。
所以![]() …………………………………①
…………………………………①
又![]() ,
,![]()
![]() ,即
,即![]()
由正弦定理得![]() ,故
,故![]() ………………………②
………………………②
由①,②解得![]() 。
。
评析:从08年高考考纲中就明确提出要加强对正余弦定理的考查.在备考中应注意总结、提高自己对问题的分析和解决能力及对知识的灵活运用能力.另外提醒:两纲中明确不再考的知识和方法了解就行,不必强化训练。 www.ks5u.com
www.ks5u.com


科目:高中数学 来源:2015届河南省高二上学期期中考试文科数学试卷(解析版) 题型:选择题
在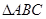 中,内角A,B,C所对的边分别是
中,内角A,B,C所对的边分别是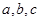 ,已知8b=5c,C=2B,则cosC=( )
,已知8b=5c,C=2B,则cosC=( )
A.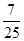 B.
B.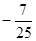 C.
C.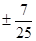 D.
D. 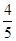
查看答案和解析>>
科目:高中数学 来源:2014届江苏省高二上期末文理数学试卷(选修)(解析版) 题型:解答题
(本题满分14分)
在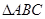 中,内角A、B、C的对边分别是
中,内角A、B、C的对边分别是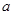 、b、c,已知
、b、c,已知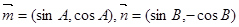 ,且
,且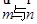 的夹角为
的夹角为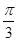 。
。
(Ⅰ)求内角C的大小;
(Ⅱ)已知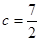 ,三角形的面积
,三角形的面积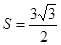 ,求
,求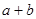 的值。
的值。
查看答案和解析>>
科目:高中数学 来源:2010-2011学年北京市海淀区高三下学期期中考试数学理卷 题型:解答题
(本小题共13分)
在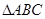 中,内角A、B、C所对的边分别为
中,内角A、B、C所对的边分别为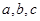 ,已知
,已知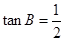 ,
,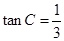 ,且
,且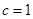 .
.
(Ⅰ)求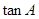 ;
;
(Ⅱ)求 的面积.
的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com