
【题目】在三棱柱![]() 中,底面
中,底面![]() 是以
是以![]() 为斜边的等腰直角三角形,侧面
为斜边的等腰直角三角形,侧面![]() 是菱形且与底面
是菱形且与底面![]() 垂直,
垂直,![]() ,点
,点![]() 是
是![]() 中点,点
中点,点![]() 是
是![]() 上靠近
上靠近![]() 点的三等分点.
点的三等分点.
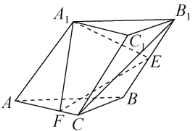
(1)证明:![]() 平面
平面![]() ;
;
(2)求二面角![]() 的余弦值.
的余弦值.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)连接![]() 交
交![]() 交于
交于![]() ,连接
,连接![]() ,通过证明
,通过证明![]() //
//![]() ,即可得证线面平行;
,即可得证线面平行;
(2)以![]() 中点
中点![]() ,建立空间直角坐标系,求得两个平面的法向量,通过向量法即可求得二面角的余弦值.
,建立空间直角坐标系,求得两个平面的法向量,通过向量法即可求得二面角的余弦值.
(1)连接![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() .
.
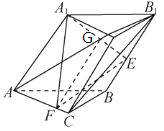
因为![]() ,所以
,所以![]() ,
,
又因为![]() ,所以
,所以![]() ,所以
,所以![]() ,
,
又![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .
.
(2)过![]() 作
作![]() 于
于![]() ,
,
因为![]() ,所以
,所以![]() 是线段
是线段![]() 的中点.
的中点.
因为平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() ,连接
,连接![]() ,
,
因为![]() 是等边三角形,
是等边三角形,![]() 是线段
是线段![]() 的中点,所以
的中点,所以![]() .
.
所以![]() 平面
平面![]() .
.
如图,以![]() 为原点,
为原点,![]() ,
,![]() ,
,![]() 所在直线
所在直线
分别为![]() 轴,
轴,![]() 轴,
轴,![]() 轴建立空间直角坐标,
轴建立空间直角坐标,

不妨设![]() ,则
,则![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
由![]() ,得
,得![]() ,
,
则![]() 的中点
的中点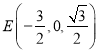 ,
,
从而![]()
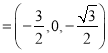 ,
,![]()
![]() .
.
设平面![]() 的法向量为
的法向量为![]()
![]() ,
,
则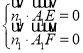 ,即
,即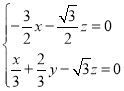 ,
,
不妨取![]() ,得
,得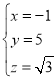 ,即
,即![]()
![]() .
.
易知平面![]() 的一个法向量为
的一个法向量为![]()
![]() ,
,
则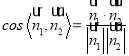
![]() ,
,
所以二面角![]() 的余弦值为
的余弦值为![]() .
.


科目:高中数学 来源: 题型:
【题目】造纸术、印刷术、指南针、火药被称为中国古代四大发明,此说法最早由英国汉学家艾约瑟提出并为后来许多中国的历史学家所继承,普遍认为这四种发明对中国古代的政治,经济,文化的发展产生了巨大的推动作用.某小学三年级共有学生500名,随机抽查100名学生并提问中国古代四大发明,能说出两种发明的有45人,能说出3种及其以上发明的有32人,据此估计该校三级的500名学生中,对四大发明只能说出一种或一种也说不出的有( )
A.69人B.84人C.108人D.115人
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学拟在高一下学期开设游泳选修课,为了了解高一学生喜欢游泳是否与性别有关,现从高一学生中抽取![]() 人做调查,得到
人做调查,得到![]() 列联表:
列联表:
喜欢游泳 | 不喜欢游泳 | 合计 | |
男生 | 40 | ||
女生 | 30 | ||
合计 | 100 |
且已知在![]() 个人中随机抽取
个人中随机抽取![]() 人,抽到喜欢游泳的学生的概率为
人,抽到喜欢游泳的学生的概率为![]() .
.
(1)请完成上面的列联表;
(2)根据列联表的数据,是否有![]() 的把握认为喜欢游泳与性别有关?并说明你的理由.
的把握认为喜欢游泳与性别有关?并说明你的理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=2ax2+2bx,若存在实数x0∈(0,t),使得对任意不为零的实数a,b均有f(x0)=a+b成立,则t的取值范围是_____.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂生产某款机器零件,因为要求精度比较高,所以需要对生产的一大批零件进行质量检测.首先由专家根据各种系数制定了质量指标值,从生产的大批零件中选取100件作为样本进行评估,根据评估结果作出如图所示的频率分布直方图.
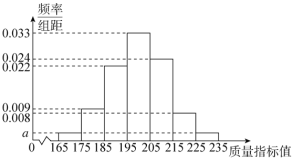
(1)(ⅰ)根据直方图求![]() 及这100个零件的样本平均数
及这100个零件的样本平均数![]() (同一组数据用该组数据区间的中点值表示);
(同一组数据用该组数据区间的中点值表示);
(ⅱ)以样本估计总体,经过专家研究,零件的质量指标值![]() ,试估计10000件零件质量指标值在
,试估计10000件零件质量指标值在![]() 内的件数;
内的件数;
(2)设每个零件利润为![]() 元,质量指标值为
元,质量指标值为![]() ,利润
,利润![]() 与质量指标值
与质量指标值![]() 之间满足函数关系
之间满足函数关系![]() .假设同组中的每个数据用该组区间的中点值代替,试估算该批零件的平均利润.(结果四舍五入,保留整数)
.假设同组中的每个数据用该组区间的中点值代替,试估算该批零件的平均利润.(结果四舍五入,保留整数)
参考数据:![]() ,则
,则![]() ,
,![]() ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】李明自主创业,在网上经营一家水果店,销售的水果中有草莓、京白梨、西瓜、桃,价格依次为60元/盒、65元/盒、80元/盒、90元/盒.为增加销量,李明对这四种水果进行促销:一次购买水果的总价达到120元,顾客就少付x元.每笔订单顾客网上支付成功后,李明会得到支付款的80%.
①当x=10时,顾客一次购买草莓和西瓜各1盒,需要支付__________元;
②在促销活动中,为保证李明每笔订单得到的金额均不低于促销前总价的七折,则x的最大值为__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥S—ABCD中,![]() 底面ABCD,底面ABCD是矩形,且
底面ABCD,底面ABCD是矩形,且![]() ,E是SA的中点.
,E是SA的中点.
(1)求证:平面BED![]() 平面SAB;
平面SAB;
(2)求平面BED与平面SBC所成二面角(锐角)的大小.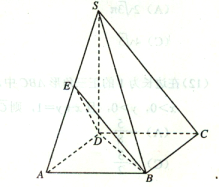
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】大荔县某高中一社团为调查学生学习围棋的情况,随机抽取了![]() 名学生进行调查.根据调查结果绘制的学生均学习围棋时间的频率分布直方图.将日均学习围棋时不低于
名学生进行调查.根据调查结果绘制的学生均学习围棋时间的频率分布直方图.将日均学习围棋时不低于![]() 分钟的学生称为“围棋迷”.
分钟的学生称为“围棋迷”.
非围棋迷 | 围棋迷 | 合计 | |
男 | |||
女 |
|
| |
合计 |

(1)根据已知条件完成下面的![]() 列联表,并据此资料你是否有
列联表,并据此资料你是否有![]() 的把握认为“围棋迷”与性别有关?
的把握认为“围棋迷”与性别有关?
(2)现在从参与本次抽样调查的![]() 名学生的男同学里面,依据是否为围棋迷,采用分层抽样的方法抽取
名学生的男同学里面,依据是否为围棋迷,采用分层抽样的方法抽取![]() 名学生参与围棋知识竞赛,再从
名学生参与围棋知识竞赛,再从![]() 人中任选
人中任选![]() 人参与知识竞赛的赛前保障工作.求选到的
人参与知识竞赛的赛前保障工作.求选到的![]() 人恰好是一个“围棋迷”和一个“非围棋迷”的概率?
人恰好是一个“围棋迷”和一个“非围棋迷”的概率?
附:![]() ,
,
|
|
|
|
|
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com