
设![]() ,
,![]() ,记
,记![]() .
.
(Ⅰ) 写出函数![]() 的最小正周期;
的最小正周期;
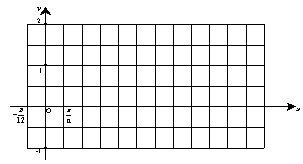
(Ⅱ) 试用“五点法”画出函数![]() 在区间
在区间![]() 的简图,并指出该函数的
的简图,并指出该函数的
图象可由![]() 的图象经过怎样的平移和伸缩变换得到?
的图象经过怎样的平移和伸缩变换得到?
 (Ⅲ) 若
(Ⅲ) 若![]() 时,函数
时,函数![]() 的最小值为2,试求出函数
的最小值为2,试求出函数![]() 的最大值并指出
的最大值并指出![]() 取何值时,函数
取何值时,函数![]() 取得最大值.
取得最大值.
科目:高中数学 来源: 题型:
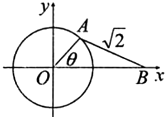 如图,已知线段AB=
如图,已知线段AB=| 2 |
| π |
| 2 |
A、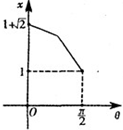 |
B、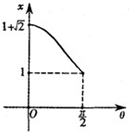 |
C、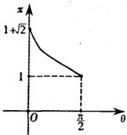 |
D、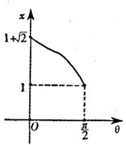 |
查看答案和解析>>
科目:高中数学 来源: 题型:
(09年海淀区期中文)(14分)
设![]() 是定义在D上的函数,若对D中的任意两个实数
是定义在D上的函数,若对D中的任意两个实数![]() ,恒有
,恒有![]() ,则称
,则称![]() 为定义在D上的T函数。
为定义在D上的T函数。
(I)试判断函数![]() 是否为其定义域上的T函数, 并说明理由;
是否为其定义域上的T函数, 并说明理由;
(II)若函数![]() 是R上的奇函数,试证明
是R上的奇函数,试证明![]() 不是R上的T函数;
不是R上的T函数;
(III)若对任何实数![]() 以及D中的任意两个实数
以及D中的任意两个实数![]() 恒有
恒有
查看答案和解析>>
科目:高中数学 来源:2010-2011学年山东省日照市实验高中高一(下)期末数学练习试卷5(必修3、4)(解析版) 题型:解答题
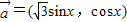 ,
,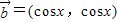 ,记
,记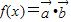 .
.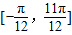 的简图,并指出该函数的图象可由y=sinx(x∈R)的图象经过怎样的平移和伸缩变换得到?
的简图,并指出该函数的图象可由y=sinx(x∈R)的图象经过怎样的平移和伸缩变换得到?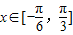 时,函数g(x)=f(x)+m的最小值为2,试求出函数g(x)的最大值并指出x取何值时,函数g(x)取得最大值.
时,函数g(x)=f(x)+m的最小值为2,试求出函数g(x)的最大值并指出x取何值时,函数g(x)取得最大值.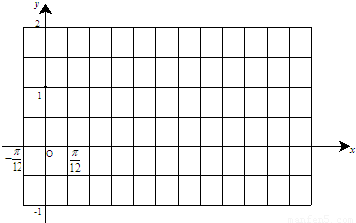
查看答案和解析>>
科目:高中数学 来源:2012-2013学年四川省成都高新区高三4月统一检测理科数学试卷(解析版) 题型:选择题
设集合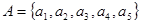 ,记
,记 是
是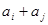 的不同值的个数,其中
的不同值的个数,其中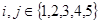 且
且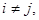
 的最大值为
的最大值为 ,
, 的最小值为
的最小值为 ,则
,则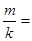 (
)
(
)
A.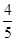 B.
B.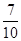 C.
C. D.
D.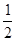
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com