
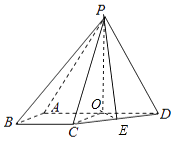
【题目】如图,四棱锥P﹣ABCD中,侧面PAD为等边三角形且垂直于底面ABCD,AB=BC= ![]() AD,∠BAD=∠ABC=90°. (Ⅰ)证明:直线BC∥平面PAD;
AD,∠BAD=∠ABC=90°. (Ⅰ)证明:直线BC∥平面PAD;
(Ⅱ)若△PAD面积为2 ![]() ,求四棱锥P﹣ABCD的体积.
,求四棱锥P﹣ABCD的体积.
【答案】(Ⅰ)证明:四棱锥P﹣ABCD中,∵∠BAD=∠ABC=90°.∴BC∥AD,∵AD平面PAD,BC平面PAD, ∴直线BC∥平面PAD;
(Ⅱ)解:四棱锥P﹣ABCD中,侧面PAD为等边三角形且垂直于底面ABCD,AB=BC= ![]() AD,∠BAD=∠ABC=90°.设AD=2x,
AD,∠BAD=∠ABC=90°.设AD=2x,
则AB=BC=x,CD= ![]() ,O是AD的中点,
,O是AD的中点,
连接PO,OC,CD的中点为:E,连接OE,
则OE= ![]() ,PO=
,PO= ![]() ,PE=
,PE= ![]() =
= ![]() ,
,
△PCD面积为2 ![]() ,可得:
,可得: ![]() =2
=2 ![]() ,
,
即: ![]() ,解得x=2,PE=2
,解得x=2,PE=2 ![]() .
.
则V P﹣ABCD= ![]() ×
× ![]() (BC+AD)×AB×PE=
(BC+AD)×AB×PE= ![]() =4
=4 ![]() .
.
【解析】(Ⅰ)利用直线与平面平行的判定定理证明即可. (Ⅱ)利用已知条件转化求解几何体的线段长,然后求解几何体的体积即可.
【考点精析】利用直线与平面平行的判定对题目进行判断即可得到答案,需要熟知平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行.


 备战中考寒假系列答案
备战中考寒假系列答案科目:高中数学 来源: 题型:
【题目】如图所示,在正方体ABCD-A1B1C1D中,S是B1D1的中点,E、F、G分别是BC、CD和SC的中点.求证:
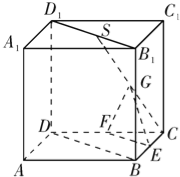
(1)直线EG∥平面BDD1B1;
(2)平面EFG∥平面BDD1B1.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,设中心在坐标原点,焦点在
中,设中心在坐标原点,焦点在![]() 轴上的椭圆
轴上的椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,右准线
,右准线![]() 与
与![]() 轴的交点为
轴的交点为![]() ,
,![]() .
.

(1)已知点![]() 在椭圆
在椭圆![]() 上,求实数
上,求实数![]() 的值;
的值;
(2)已知定点![]() .
.
① 若椭圆![]() 上存在点
上存在点![]() ,使得
,使得![]() ,求椭圆
,求椭圆![]() 的离心率的取值范围;
的离心率的取值范围;
② 如图,当![]() 时,记
时,记![]() 为椭圆
为椭圆![]() 上的动点,直线
上的动点,直线![]() 分别与椭圆
分别与椭圆![]() 交于另一点
交于另一点![]() ,若
,若![]() 且
且![]() ,求证:
,求证:![]() 为定值.
为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有一隧道内设双行线公路,其截面由一长方形和一抛物线构成,如图所示.为保证安全,要求行驶车辆顶部(设为平顶)与隧道顶部在竖直方向上高度之差至少要有![]() 米.若行车道总宽度
米.若行车道总宽度![]() 为
为![]() 米.
米.
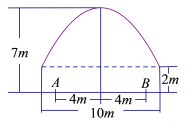
(1)计算车辆通过隧道时的限制高度;
(2)现有一辆载重汽车宽![]() 米,高
米,高![]() 米,试判断该车能否安全通过隧道?
米,试判断该车能否安全通过隧道?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在四棱锥S-ABCD中,底面ABCD是边长为1的正方形,SD![]() 底面ABCD,SD=2,其中
底面ABCD,SD=2,其中![]() 分别是
分别是![]() 的中点,
的中点,![]() 是
是![]() 上的一个动点.
上的一个动点.
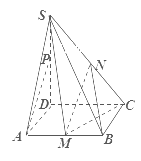
(1)当点![]() 落在什么位置时,
落在什么位置时,![]() ∥平面
∥平面![]() ,证明你的结论;
,证明你的结论;
(2)求三棱锥![]() 的体积.
的体积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com