
 (x-
(x- )或y+2=-
)或y+2=- (x-
(x- ),②
),② )或(0,-
)或(0,- ),
),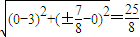 ,
, )2=
)2=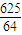 或x2+(y-
或x2+(y- )2=
)2=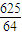 .
. )2=
)2=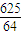 或x2+(y-
或x2+(y- )2=
)2=


科目:高中数学 来源: 题型:044
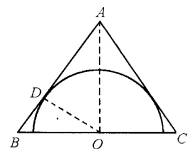
如图所示,有一等腰三角形薄铁板,其底板BC=4dm,AB=xdm,现将其按图示截取一个半圆(半圆圆心在底边上,且与两腰相切),半圆的面积为y,求函数y=f(x)的解析式及定义域.
查看答案和解析>>
科目:高中数学 来源:数学教研室 题型:044
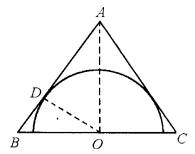
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com