解:(Ⅰ)求导函数可得f'(x)=3x
2+2(1-a)x-a(a+2)=(x-a)[3x+(a+2)],
函数f(x)在区间(-1,1)不单调,等价于导函数f′(x)在(-1,1)既能取到大于0的实数,又能取到小于0的实数,即函数f′(x)在(-1,1)上存在零点,但无重根.
令f'(x)=0得x=a与x=-

,则-1<a<1或-1<-

<1,且a≠-

,∴-5<a<1且
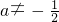
综上-5<a<-

或

<a<1;
(Ⅱ)由题意,函数f′(x)+2ax值域是g(x)的值域的子集
∵x∈[0,2],
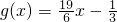
,∴g(x)∈[-

,6];
令F(x)=f′(x)+2ax=3x
2+2(1-a)x-a(a+2)+2ax=3x
2+2x-a
2-2a
∵x∈[-1,1],∴F(x)∈[-

-a
2-2a,5-a
2-2a]
∴-

-a
2-2a≥-

且5-a
2-2a≤6
∴-2≤a≤0
∴a∈[-2,0]
分析:(Ⅰ)函数f(x)在区间(-1,1)不单调,等价于导函数f′(x)在(-1,1)既能取到大于0的实数,又能取到小于0的实数,即函数f′(x)在(-1,1)上存在零点,但无重根;
(Ⅱ)由题意,函数f′(x)+2ax值域是g(x)的值域的子集,分别求出值域,再建立不等式,即可得到结论.
点评:本题考查导数知识的运用,考查函数的单调性,考查函数的值域,将问题等价转化是关键.

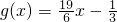 ,是否存在实数a,对任意x1∈[-1,1],存在x2∈[0,2],使得f′(x1)+2ax1=g(x2)成立?若存在,求a的值;若不存在,请说明理由.
,是否存在实数a,对任意x1∈[-1,1],存在x2∈[0,2],使得f′(x1)+2ax1=g(x2)成立?若存在,求a的值;若不存在,请说明理由. ,则-1<a<1或-1<-
,则-1<a<1或-1<- <1,且a≠-
<1,且a≠- ,∴-5<a<1且
,∴-5<a<1且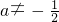
 或
或 <a<1;
<a<1;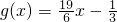 ,∴g(x)∈[-
,∴g(x)∈[- ,6];
,6]; -a2-2a,5-a2-2a]
-a2-2a,5-a2-2a] -a2-2a≥-
-a2-2a≥- 且5-a2-2a≤6
且5-a2-2a≤6

 已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<