
����Ŀ����ͼ��һ��·�Ƶ�ƽ�����ʾ��ͼ���������߶�AOB����Ϊ�����ߵ�һ���֣�����ԭ��OΪ�����ߵĶ��㣬�����ߵĶԳ���Ϊy�ᣬ�Ƹ�BC����Ϊ�߶Σ�������ֱ��������AOB���ڵ������������ڵ�B.��֪AB=2���ף�ֱ��![]() �ᣬ��C��ֱ��AB�ľ���Ϊ8����.�Ƹ�BC���ֵ����Ϊ10Ԫ/���ף�������O��ֱ��AB�ľ���Ϊt���ף������߶�AOB���ֵ����Ϊ
�ᣬ��C��ֱ��AB�ľ���Ϊ8����.�Ƹ�BC���ֵ����Ϊ10Ԫ/���ף�������O��ֱ��AB�ľ���Ϊt���ף������߶�AOB���ֵ����Ϊ![]() Ԫ. ��ֱ��BC����б��Ϊ�����������ֵ������ΪSԪ.
Ԫ. ��ֱ��BC����б��Ϊ�����������ֵ������ΪSԪ.
��1������t�����ĺ�����ϵʽ��
����S�����ĺ�����ϵʽ��
��2���������S����Сֵ.


���𰸡�(1) �� ![]() .��
.��![]() .
.
(2) ![]() Ԫ.
Ԫ.
����������������1�����������߶�![]() ���ڵ������ߵķ���Ϊ
���ڵ������ߵķ���Ϊ![]() �������B�ɵ�a��ֵ��Ȼ���������BC��б��,ת��Ϊ��б�Ǵӽ���t��
�������B�ɵ�a��ֵ��Ȼ���������BC��б��,ת��Ϊ��б�Ǵӽ���t��![]() �ĵ�ʽ��ϵ���ڸ���t��
�ĵ�ʽ��ϵ���ڸ���t��![]() �Ĺ�ϵ�ó����߶�
�Ĺ�ϵ�ó����߶�![]() ���ֵ����Ϊ
���ֵ����Ϊ![]() Ԫ��Ȼ�����BC�ε���ۣ���
Ԫ��Ȼ�����BC�ε���ۣ���![]() ���ε����֮�ͣ���2����S�ı���ʽ���ݵ���ȷ�������ĵ����ԣ����������Сֵ.
���ε����֮�ͣ���2����S�ı���ʽ���ݵ���ȷ�������ĵ����ԣ����������Сֵ.
��⣺
��1���������߶�![]() ���ڵ������ߵķ���Ϊ
���ڵ������ߵķ���Ϊ![]() ����
����![]() ����
����![]() ��
��![]() ���������ߵķ���Ϊ
���������ߵķ���Ϊ![]() ����
����![]() ��������
��������![]() ��б��Ϊ
��б��Ϊ![]() ����ֱ��
����ֱ��![]() ����б��Ϊ����
����б��Ϊ����![]() ��t�����ĺ�����ϵΪ
��t�����ĺ�����ϵΪ![]() .
.
����Ϊ![]() ���������߶�
���������߶�![]() ���ֵ����Ϊ
���ֵ����Ϊ![]() Ԫ��
Ԫ��
��Ϊ��![]() ��ֱ��
��ֱ��![]() �ľ���Ϊ8���ף�ֱ��
�ľ���Ϊ8���ף�ֱ��![]() ����б��Ϊ����
����б��Ϊ����![]() ��
��![]() ���ֵ����Ϊ
���ֵ����Ϊ![]() ��
��
�������ֵ������Ϊ![]() ��
��![]() .
.
��2��![]() ��
��![]()
![]() ��
��
����![]() ���������
���������![]() ��
��![]() ����
����![]() ��
��![]() Ϊ��ǣ�
Ϊ��ǣ�
�б����£�
|
|
|
|
|
| 0 |
|
|
| ��С |
|
�ʵ�![]() ʱ
ʱ![]() ����Сֵ����ʱ
����Сֵ����ʱ![]() ��
��![]() ��
��![]() ��
��
�������S����СֵΪ![]() Ԫ.
Ԫ.


 ���Ž�������С״Ԫϵ�д�
���Ž�������С״Ԫϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪![]() ͼ������һ��͵�
ͼ������һ��͵�![]() ����ͼ���ϸ��������겻�䣬��������Ϊԭ����
����ͼ���ϸ��������겻�䣬��������Ϊԭ����![]() ����������ƽ��
����������ƽ��![]() ����λ��
�����![]() ����
����![]() ������������������
�����и���С�����������![]() ����λ����
����λ����![]() �Ľ���ʽΪ__________.
�Ľ���ʽΪ__________.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������![]() ��
��![]() ��
��![]() ���Ľ���Ϊ
���Ľ���Ϊ![]() ���������ϴ���һ��
���������ϴ���һ��![]() ������ľ���Ϊ3���ҵ�
������ľ���Ϊ3���ҵ�![]() ��Բ
��Բ![]() ��
��![]() ��.
��.
������������![]() �ķ��̣�
�ķ��̣�
������֪��Բ![]() ��
��![]() ��
��![]() ����һ��������������
����һ��������������![]() �Ľ����غϣ���������Ϊ
�Ľ����غϣ���������Ϊ![]() .ֱ��
.ֱ��![]() ��
��![]() ����Բ
����Բ![]() ��
��![]() ��
��![]() ������ͬ�ĵ㣬��ԭ��
������ͬ�ĵ㣬��ԭ��![]() �����߶�
�����߶�![]() Ϊֱ����Բ���ⲿ����ʵ��
Ϊֱ����Բ���ⲿ����ʵ��![]() ��ȡֵ��Χ.
��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����Ŀ�ѧ��������֪����![]() ����
����![]() .
.
��1����![]() ��
��![]() ��
��![]() ��ֵ�����벢֤��
��ֵ�����벢֤��![]() �ĵ����ԣ�
�ĵ����ԣ�
��2�����÷�֤��֤������![]() ������������ܹ��ɵȲ����У�
������������ܹ��ɵȲ����У�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������P��ABCD�У�����ABCDΪ�����Σ�PA�͵���ABCD��AD=AP��EΪ��PD�е㣮
��1����֤��PD��ƽ��ABE��
��2����FΪAB�е㣬 ![]() ����ȷ���˵�ֵ��ʹ�����P��FM��B������ֵΪ-
����ȷ���˵�ֵ��ʹ�����P��FM��B������ֵΪ- ![]() ��
�� 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ��ij�ֵ���ί������![]() �ضεľ���¥���Ϸ���Ŀհض�
�ضεľ���¥���Ϸ���Ŀհض�![]() �Ͻ�һ������ģ�����
�Ͻ�һ������ģ�����![]() �ף�����Ķ������������¥ƽ��. �Ӷ�����������ĵĽ���ͼ���²����dz�����
�ף�����Ķ������������¥ƽ��. �Ӷ�����������ĵĽ���ͼ���²����dz�����![]() ���ϲ�������
���ϲ�������![]() Ϊֱ���İ�Բ. Ϊ�˱�֤����¥ס���IJɹ�Ҫ����������Բ���е�̫���������������ھ���¥�ϵ�Ӱ��
Ϊֱ���İ�Բ. Ϊ�˱�֤����¥ס���IJɹ�Ҫ����������Բ���е�̫���������������ھ���¥�ϵ�Ӱ��![]() ������
������![]() �ף����и�̫��������ˮƽ�ߵļн�
�ף����и�̫��������ˮƽ�ߵļн�![]() ����
����![]() .
.

��1�������![]() �ף�
�ף�![]() �ף����ܷ�֤�����ɹ�Ҫ��
�ף����ܷ�֤�����ɹ�Ҫ��
��2���ڱ�֤�����ɹ�Ҫ���ǰ���£�������![]() ��
��![]() �ij��ȣ���ʹ�û���ĵĽ���������ע��������
�ij��ȣ���ʹ�û���ĵĽ���������ע��������![]() ȡ3��
ȡ3��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������{an}����a1+a2+a3+��an=2n��an��n��N+��������{bn}����bn= ![]() ����{bn}�е�������ֵ�� ��
����{bn}�е�������ֵ�� ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ˮ�ǵ����ϱ������Դ�����ڽ���Ƚϱ����ںܶȱˮ�ij��о������Ƶ�ʹ��ˮ��Դ������ص���Դ�˷ѣ�ij������Ϊ���ᳫ��̼����������������������Լ��ˮ���ƻ���������������ˮ�շѷ�������ȷ��һ������������ˮ����x���֣���һλ���������ˮ��������x�IJ��ְ�ƽ���շѣ�����x�IJ��ְ�����շѣ�Ϊ���˽������ˮ�����ͨ�������������ij��100λ����ÿ�˵��¾���ˮ������λ���֣��������ݰ���[0��0.5����[0.5��1����[1��1.5��������[4��4.5���ֳ�9�飬�Ƴ�����ͼ��ʾ��Ƶ�ʷֲ�ֱ��ͼ�� 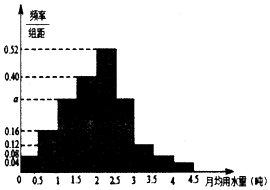
��1����ȫ�о������¾���ˮ��������3�ֵ�����Ϊ3.6���Թ���ȫ���ж��پ���˵�����ɣ�
��2���������������ȡ�ֲ�����ķ�������ˮ������Ϊ[1��1.5����[1.5��2��֮��ѡȡ7��������Ϊ���ˮ�Ѽ۸���֤��Ĵ�����������������7����ͥ�а���ǩ��ʽѡ��4���䷢����̼������ͥ��������XΪ��ˮ��������[1��1.5���еĻļ�ͥ����YΪ��ˮ��������[1.5��2���еĻ�ͥ�������������Z=|X��Y|����Z�ķֲ��к���ѧ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com