
【题目】已知集合![]() .
.
(1)证明:若![]() ,则
,则![]() ,
,![]() ;
;
(2)证明:若![]() ,则
,则![]() ,并由此证明
,并由此证明![]() 中的元素
中的元素![]() 若满足
若满足![]() ,则
,则![]() ;
;
(3)设![]() ,试求满足
,试求满足![]() 的所有
的所有![]() 的可能值.
的可能值.
【答案】(1)证明见解析 (2)证明见解析 (3)c=7+4![]()
【解析】
(1)若![]() ,则
,则![]() 且
且![]() ,
,![]() ,
,![]() ,得到
,得到![]() ,
,![]() 均满足集合
均满足集合![]() 的性质,进而得到结论.
的性质,进而得到结论.
(2)构造函数![]() ,分析其单调性,进而得到
,分析其单调性,进而得到![]() 中元素若满足
中元素若满足![]() ,则
,则![]() .
.
(3)设![]() ,结合(1)(2)中的结论,可得
,结合(1)(2)中的结论,可得![]() 值.
值.
证明:(1)若a∈A,则a=m+n![]() 且m2﹣3n2=1,m,n∈Z,
且m2﹣3n2=1,m,n∈Z,
则![]() m+(﹣n)
m+(﹣n)![]() 且m2﹣3(﹣n)2=1,m,﹣n∈Z,
且m2﹣3(﹣n)2=1,m,﹣n∈Z,
故![]() ∈A,
∈A,
则![]() (m+n
(m+n![]() )=(2m﹣3n)+(2n﹣m)
)=(2m﹣3n)+(2n﹣m)![]() ,
,
此时(2m﹣3n)2﹣3
故![]() ∈A;
∈A;
(2)令f(x)=x![]() (x≥1),则
(x≥1),则![]() 在
在![]() 上的单调递增,
上的单调递增,
证明:设![]() ,
,
则![]()
∵ ![]() ,
,
∴![]()
![]() ,
,![]()
![]() ,
,
故![]()
![]() ,即
,即![]() ,
,![]() 在
在![]() 上的单调递增
上的单调递增
∵1<p≤q,f(1)=2
∴2![]() ;
;
令b=m+n![]() 且m2﹣3n2=1,m,n∈Z,
且m2﹣3n2=1,m,n∈Z,
∵1![]() ,
,
∴2<b![]() ,
,
∴2<2m≤4,
则m=2,n=1,则b=2![]() ;
;
(3)∵c∈A,且2![]() c≤(2
c≤(2![]() )2,
)2,
∴![]() ∈A,且1
∈A,且1![]() 2
2![]() ,
,
由(2)得:![]() 2
2![]() ,
,
∴c=(2![]() )2=7+4
)2=7+4![]()


科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 中心在坐标原点,焦点在
中心在坐标原点,焦点在![]() 轴上,且过
轴上,且过![]() ,直线
,直线![]() 与椭圆交于
与椭圆交于![]() ,
,![]() 两点(
两点(![]() ,
,![]() 两点不是左右顶点),若直线
两点不是左右顶点),若直线![]() 的斜率为
的斜率为![]() 时,弦
时,弦![]() 的中点
的中点![]() 在直线
在直线![]() 上.
上.
(Ⅰ)求椭圆![]() 的方程.
的方程.
(Ⅱ)若以![]() ,
,![]() 两点为直径的圆过椭圆的右顶点,则直线
两点为直径的圆过椭圆的右顶点,则直线![]() 是否经过定点,若是,求出定点坐标,若不是,请说明理由.
是否经过定点,若是,求出定点坐标,若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,三条直线型公路![]() ,
,![]() ,
,![]() 在点
在点![]() 处交汇,其中
处交汇,其中![]() 与
与![]() 、
、![]() 与
与![]() 的夹角都为
的夹角都为![]() ,在公路
,在公路![]() 上取一点
上取一点![]() ,且
,且![]() km,过
km,过![]() 铺设一直线型的管道
铺设一直线型的管道![]() ,其中点
,其中点![]() 在
在![]() 上,点
上,点![]() 在
在![]() 上(
上(![]() ,
,![]() 足够长),设
足够长),设![]() km,
km,![]() km.
km.
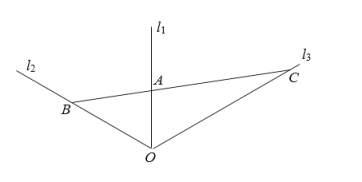
(1)求出![]() ,
,![]() 的关系式;
的关系式;
(2)试确定![]() ,
,![]() 的位置,使得公路
的位置,使得公路![]() 段与
段与![]() 段的长度之和最小.
段的长度之和最小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,函数
,函数![]() 的图像为直线
的图像为直线![]() .
.
(Ⅰ)当![]() 时,若函数
时,若函数![]() 的图像永远在直线
的图像永远在直线![]() 下方,求实数
下方,求实数![]() 的取值范围;
的取值范围;
(Ⅱ)当![]() 时,若直线
时,若直线![]() 与函数
与函数![]() 的图像的有两个不同的交点
的图像的有两个不同的交点![]() ,线段
,线段![]() 的中点为
的中点为![]()
![]() ,求证:
,求证:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某创业团队拟生产![]() 两种产品,根据市场预测,
两种产品,根据市场预测,![]() 产品的利润与投资额成正比(如图1),
产品的利润与投资额成正比(如图1),![]() 产品的利润与投资额的算术平方根成正比(如图2).(注: 利润与投资额的单位均为万元)
产品的利润与投资额的算术平方根成正比(如图2).(注: 利润与投资额的单位均为万元)

(注:利润与投资额的单位均为万元)
(1)分別将![]() 两种产品的利润
两种产品的利润![]() 、
、![]() 表示为投资额
表示为投资额![]() 的函数;
的函数;
(2)该团队已筹集到10 万元资金,并打算全部投入![]() 两种产品的生产,问:当
两种产品的生产,问:当![]() 产品的投资额为多少万元时,生产
产品的投资额为多少万元时,生产![]() 两种产品能获得最大利润,最大利润为多少?
两种产品能获得最大利润,最大利润为多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地级市共有200000中小学生,其中有7%学生在2017年享受了“国家精准扶贫”政策,在享受“国家精准扶贫”政策的学生中困难程度分为三个等次:一般困难、很困难、特别困难,且人数之比为5:3:2,为进一步帮助这些学生,当地市政府设立“专项教育基金”,对这三个等次的困难学生每年每人分别补助1000元、1500元、2000元。经济学家调查发现,当地人均可支配年收入较上一年每增加![]() ,一般困难的学生中有
,一般困难的学生中有![]() 会脱贫,脱贫后将不再享受“精准扶贫”政策,很困难的学生中有
会脱贫,脱贫后将不再享受“精准扶贫”政策,很困难的学生中有![]() 转为一般困难,特别困难的学生中有
转为一般困难,特别困难的学生中有![]() 转为很困难。现统计了该地级市2013年到2017年共5年的人均可支配年收入,对数据初步处理后得到了如图所示的散点图和表中统计量的值,其中年份
转为很困难。现统计了该地级市2013年到2017年共5年的人均可支配年收入,对数据初步处理后得到了如图所示的散点图和表中统计量的值,其中年份![]() 取13时代表2013年,
取13时代表2013年, ![]() 与
与![]() (万元)近似满足关系式
(万元)近似满足关系式![]() ,其中
,其中![]() 为常数。(2013年至2019年该市中学生人数大致保持不变)
为常数。(2013年至2019年该市中学生人数大致保持不变)


其中![]() ,
, ![]()
(Ⅰ)估计该市2018年人均可支配年收入;
(Ⅱ)求该市2018年的“专项教育基金”的财政预算大约为多少?
附:对于一组具有线性相关关系的数据![]() ,其回归直线方程
,其回归直线方程 ![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com