Question

【题目】已知椭圆的两焦点为，，离心率.

（1）求此椭圆的方程；

（2）设直线：，若与此椭圆相交于，两点，且等于椭圆的短轴长，求的值；

（3）以此椭圆的上顶点为直角顶点作椭圆的内接等腰直角三角形，这样的直角三角形是否存在？若存在，请说明有几个；若不存在，请说明理由.

Answer 1

【答案】(1);(2);(3)见解析.

【解析】

（1）由题设条件椭圆的两焦点为，，离心率，求出，两参数的值，即可求得椭圆的方程；（2）根据直线与此椭圆相交于，两点，且等于椭圆的短轴长，故可由弦长公式建立方程求出参数的值．首先要将直线方程与椭圆方程联立，再利用弦长公式建立方程，即可求解；（3）先假设能构成等腰直角三角形，其中，由题意可知，直角边，不可能垂直或平行于轴，故可设边所在直线的方程为（不妨设），则边所在直线的方程为，将此两直线方程与椭圆的方程联立，分别解出，两点的坐标，用坐标表示出两线段，的长度，由两者相等建立方程求参数，由解的个数判断三角形的个数即可．

（1）设椭圆方程为，

则，，

所求椭圆方程为.

（2）由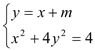，消去y，得，

则得 （*）

设，则，，

，

解得.，满足（*）

(3)设能构成等腰直角三角形，其中，由题意可知，直角边，不可能垂直或平行于轴，故可设边所在直线的方程为（不妨设），则边所在直线的方程为.

由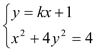，得A

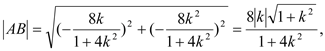
用代替上式中的k，得，

由，得

k<0，解得或，

故存在三个内接等腰直角三角形.