练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知，，满足．

    （1）将表示为的函数，并求的最小正周期；

    （2）已知、、分别为锐角的三个内角、、对应的边长，的最大值是，且，求周长的取值范围．

    【答案】（1），最小正周期为；（2）.

    【解析】

    （1）由，可得出，利用二倍角降幂公式以及辅助角公式可将函数的解析式化简，然后利用周期公式可计算出函数的最小正周期；

    （2）由题意可得，可得出的取值范围，结合题中条件求出的值，然后利用正弦定理将表示为角的三角函数，并求出角的取值范围，利用正弦函数的基本性质可求出的取值范围.

    （1），，满足，

    ，

    ，

    因此，函数的最小正周期为；

    （2）由题意可知，函数的最大值为.

    为锐角，则，，则，解得.

    由正弦定理，，，

    ，

    为锐角三角形，且，则，即，解得，

    ，，则.

    因此，的周长的取值范围是.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】在平面直角坐标系中，直线l的参数方程为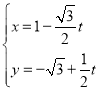（t为参数）.以坐标原点为极点，以x轴的正半轴为极轴，建立极坐标系.曲线C的极坐标方程为.

    （1）求直线l的普通方程及曲线C的直角坐标方程；

    （2）设点，直线l与曲线C相交于A，B两点，求的值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知数列中，已知，对任意都成立，数列的前n项和为．

    （1）若是等差数列，求k的值；

    （2）若，，求；

    （3）是否存在实数k，使数列是公比不为1的等比数列，且任意相邻三项，，按某顺序排列后成等差数列？若存在，求出所有k的值；若不存在，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

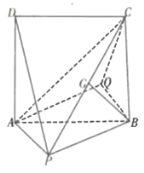
    【题目】如图所示的几何体中，正方形所在平面垂直于平面，四边形为平行四边形，为上一点，且平面，.

    （1）求证：平面平面；

    （2）当三棱锥体积最大时，求直线与平面所成角的正切值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】根据阅兵领导小组办公室介绍，2019年国庆70周年阅兵有59个方(梯)队和联合军乐团，总规模约1．5万人，是近几次阅兵中规模最大的一次．其中，徒步方队15个．为了保证阅兵式时队列保持整齐，各个方队对受阅队员的身高也有着非常严格的限制，太高或太矮都不行．徒步方队队员，男性身高普遍在175cm至185cm之间；女性身高普遍在163cm至175cm之间，这是常规标准．要求最为严格的三军仪仗队，其队员的身高一般都在184cm至190cm之间．经过随机调查某个阅兵阵营中女子100人，得到她们身高的直方图，如图，记C为事件：“某一阅兵女子身高不低于169cm”，根据直方图得到P(C)的估计值为0．5．

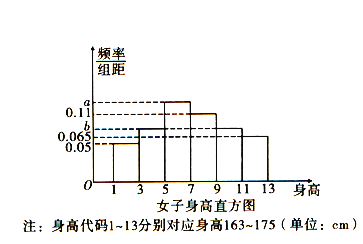
    (1)求直方图中a，b的值；

    (2)估计这个阵营女子身高的平均值 (同一组中的数据用该组区间的中点值为代表)

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设是两条不同的直线，是两个不同的平面，则下列命题中正确命题的序号是（ ）

    ①若直线平行于平面内的无数条直线，则直线∥平面.

    ②若直线∥平面，直线∥直线，则直线平行于平面内的无数条直线.

    ③若直线不平行，则不可能垂直于同一平面.

    ④若直线∥平面，平面平面，则直线平面

    A.①②B.②③C.②④D.③④

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在数列中，，且.

    （1）的通项公式为__________；

    （2）在、、、、这项中，被除余的项数为__________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设函数，其中，若、、是的三条边长，则下列结论：①对于一切都有；②存在使、、不能构成一个三角形的三边长；③为钝角三角形，存在，使，其中正确的个数为______个

    A. 3B. 2C. 1D. 0

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某城市有东、西、南、北四个进入城区主干道的入口，在早高峰时间段，时常发生交通拥堵，交警部门记录了11月份30天内的拥堵情况（如下表所示，其中●表示拥堵，○表示通畅）.假设每个人口是否发生拥堵相互独立，将各入口在这30天内拥堵的频率代替各入口每天拥堵的概率.

    11.1

    11.2

    11.3

    11.4

    11.5

    11.6

    11.7

    11.8

    11.9

    11.10

    11.11

    11.12

    11.13

    11.14

    11.15

    东入口

    ●

    ○

    ○

    ○

    ○

    ●

    ○

    ●

    ●

    ○

    ●

    ●

    ●

    ○

    ●

    西入口

    ○

    ○

    ●

    ●

    ○

    ●

    ○

    ●

    ○

    ●

    ○

    ●

    ●

    ○

    ○

    南入口

    ○

    ●

    ○

    ○

    ○

    ●

    ○

    ○

    ○

    ○

    ○

    ○

    ○

    ○

    ●

    北入口

    ●

    ○

    ○

    ○

    ●

    ○

    ○

    ●

    ○

    ○

    ○

    ○

    ○

    ●

    ○

    11.16

    11.17

    11.18

    11.19

    11.20

    11.21

    11.22

    11.23

    11.24

    11.25

    11.26

    11.27

    11.28

    11.29

    11.30

    东入口

    ●

    ○

    ○

    ●

    ○

    ○

    		p>○

    ●

    ●

    ○

    ●

    ○

    ●

    ○

    ●

    西入口

    ●

    ○

    ●

    ●

    ○

    ●

    ○

    ●

    ○

    ●

    ○

    ●

    ○

    ●

    ○

    南入口

    ○

    ○

    ○

    ●

    ○

    ○

    ○

    ○

    ●

    ○

    ○

    ○

    ○

    ○

    ●

    北入口

    ○

    ○

    ●

    ○

    ○

    ○

    ○

    ○

    ○

    ○

    ○

    ○

    ○

    ●

    ○

    （1）分别求该城市一天中早高峰时间段这四个主干道的入口发生拥堵的概率.

    （2）各人口一旦出现拥堵就需要交通协管员来疏通，聘请交通协管员有以下两种方案可供选择.方案一：四个主干道入口在早高峰时间段每天各聘请一位交通协管员，聘请每位交通协管员的日费用为（，且）元.方案二：在早高峰时间段若某主干道入口发生拥堵，交警部门则需临时调派两位交通协管员协助疏通交通，调派后当日需给每位交通协管员的费用为200元.以四个主干道入口聘请交通协管员的日总费用的数学期望为依据，你认为在这两个方案中应该如何选择？请说明理由.

    查看答案和解析>>

    同步练习册答案