
 ,
, .
.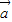 ⊥
⊥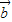 ”为事件A,求事件A发生的概率;
”为事件A,求事件A发生的概率;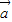 与
与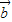 所成角为钝角”为事件B,求事件B发生的概率.
所成角为钝角”为事件B,求事件B发生的概率.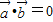 的所有数组,运用古典概型求事件A发生的概率;
的所有数组,运用古典概型求事件A发生的概率;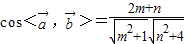 知,
知,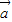 与
与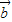 所成角为钝角,则2m+n<0,除去使余弦值为-1的角,结合m∈[-1,2],n∈[-1,1]求出m和n所满足的条件,运用几何概型求事件B发生的概率.
所成角为钝角,则2m+n<0,除去使余弦值为-1的角,结合m∈[-1,2],n∈[-1,1]求出m和n所满足的条件,运用几何概型求事件B发生的概率.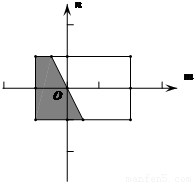 解:(I)有序数组(m,n)的所有可能结果为:(-2,-2),(-2,-1),(-2,1),(-2,2),
解:(I)有序数组(m,n)的所有可能结果为:(-2,-2),(-2,-1),(-2,1),(-2,2),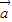 ⊥
⊥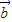 成立的( m,n ),满足:2m+n=0,n=-2m
成立的( m,n ),满足:2m+n=0,n=-2m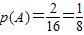 .
.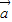 与
与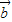 所成角为钝角成立的( m,n )满足:2m+n<0,且mn≠2.
所成角为钝角成立的( m,n )满足:2m+n<0,且mn≠2.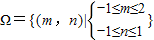 ,
,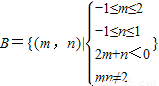 ,区域如图所示,
,区域如图所示,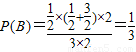 .
.

 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案科目:高中数学 来源: 题型:阅读理解
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
|
|
| a | 2 1 |
| a | 2 2 |
| a | 2 3 |
| b | 2 1 |
| b | 2 2 |
| b | 2 3 |
| x |
| 2x-2 |
| 8-3x |
查看答案和解析>>
科目:高中数学 来源: 题型:
| a |
| b |
| a |
| b |
| a |
| b |
查看答案和解析>>
科目:高中数学 来源: 题型:
| a |
| 3 |
| b |
| 1 |
| 2 |
| ||
| 2 |
| π |
| 2 |
| π |
| 2 |
| c |
| a |
| b |
| d |
| a |
| b |
| c |
| d |
查看答案和解析>>
科目:高中数学 来源:2012-2013学年四川省成都四中高三(上)期中数学试卷(文科)(解析版) 题型:解答题
 ,
,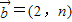 .
.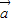 ⊥
⊥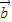 ”为事件A,求事件A发生的概率;
”为事件A,求事件A发生的概率; 与
与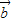 所成角为钝角”为事件B,求事件B发生的概率.
所成角为钝角”为事件B,求事件B发生的概率.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com