
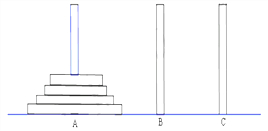
 古代印度婆罗门教寺庙内的僧侣们曾经玩过一种被称为“河内宝塔问题”的游戏,其玩法如下:如图,设有n(n∈N*)个圆盘依其半径大小,大的在下,小的在上套在A柱上,现要将套在A柱上的盘换到C柱上,要求每次只能搬动一个,而且任何时候不允许将大盘套在小盘上面,假定有三根柱子A、B、C可供使用.现用an表示将n个圆盘全部从A柱上移到C柱上所至少需要移动的次数,回答下列问题:
古代印度婆罗门教寺庙内的僧侣们曾经玩过一种被称为“河内宝塔问题”的游戏,其玩法如下:如图,设有n(n∈N*)个圆盘依其半径大小,大的在下,小的在上套在A柱上,现要将套在A柱上的盘换到C柱上,要求每次只能搬动一个,而且任何时候不允许将大盘套在小盘上面,假定有三根柱子A、B、C可供使用.现用an表示将n个圆盘全部从A柱上移到C柱上所至少需要移动的次数,回答下列问题: |
| 1≤i≤j≤n |
 |
| 1≤i≤j≤n |
| 1 |
| 7 |
| S1 |
| S2 |
| S1•S3 |
| S2•S4 |
| S1•S3…S2n-1 |
| S2•S4…S2n |
| 4 |
| 21 |
 |
| 1≤i≤j≤n |
| 4 |
| 3 |
| S1•S3•…•S2n-1 |
| S2•S4•…•S2n |
|
 |
| 1≤i≤j≤n |
| 1 |
| 2 |
| b | 2 1 |
| b | 2 2 |
| b | 2 n |
|
| S1•S3•…•S2n-1 |
| S2•S4•…•S2n |
| S1•S3…S2n-1 |
| S2•S4…S2n |
| (21-1)(22-1) |
| (22-1)(23-1) |
| (23-1)(24-1) |
| (24-1)(25-1) |
| (22n-1-1)(22n-1) |
| (22n-1)(22n+1-1) |
|
| 1 |
| 23-1 |
| 1 |
| 7 |
| 4 |
| 21 |
|
|
|
| 1 |
| 7 |
| S1 |
| S2 |
| S1•S3 |
| S2•S4 |
| S1•S3•…•S2n-1 |
| S2•S4•…•S2n |
| 4 |
| 21 |


科目:高中数学 来源: 题型:

 |
| 1≤i≤j≤n |
 |
| 1≤i≤j≤n |
| S1 |
| S2 |
| S2 |
| S3 |
| Sn |
| Sn+1 |
| n |
| 4 |
| 3 |
| 16 |
| 3 |
| 16 |
| 1 |
| 2n |
查看答案和解析>>
科目:高中数学 来源: 题型:
古代印度婆罗门教寺庙内的僧侣们曾经玩过一种被称为“河内宝塔问题”的游戏,其玩法如下:如图,设有![]() 个圆盘依其半径大小,大的在下,小的在上套在
个圆盘依其半径大小,大的在下,小的在上套在![]() 柱上,现要将套在
柱上,现要将套在![]() 柱上的盘换到
柱上的盘换到![]() 柱上,要求每次只能搬动一个,而且任何时候不允许将大盘套在小盘上面,假定有三根柱子
柱上,要求每次只能搬动一个,而且任何时候不允许将大盘套在小盘上面,假定有三根柱子![]() 可供使用.
可供使用.

现用![]() 表示将
表示将![]() 个圆盘全部从
个圆盘全部从![]() 柱上移到
柱上移到![]() 柱上所至少需要移动的次数,回答下列问题:
柱上所至少需要移动的次数,回答下列问题:
(1)写出![]() 并求出
并求出![]()
(2)记![]() 求和
求和![]() (其中
(其中![]() 表示所有的积
表示所有的积![]() 的和)
的和)
(3)证明:![]()
查看答案和解析>>
科目:高中数学 来源:2010年重庆市西南师大附中高三下学期五月月考数学(理) 题型:解答题
(本小题满分12分)
古代印度婆罗门教寺庙内的僧侣们曾经玩过一种被称为“河内宝塔问题”的游戏,其玩法如下:如图,设有n( )个圆盘依其半径大小,大的在下,小的在上套在A柱上,现要将套在A柱上的盘换到C柱上,要求每次只能搬动一个,而且任何时候不允许将大盘套在小盘上面,假定有三根柱子A、B、C可供使用.
)个圆盘依其半径大小,大的在下,小的在上套在A柱上,现要将套在A柱上的盘换到C柱上,要求每次只能搬动一个,而且任何时候不允许将大盘套在小盘上面,假定有三根柱子A、B、C可供使用.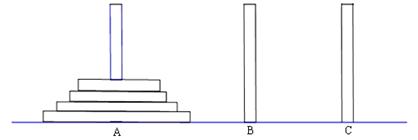
现用an表示将n个圆盘全部从A柱上移到C柱上所至少需要移动的次数,回答下列问题:
(1) 写出a1,a2,a3,并求出an;
(2) 记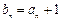 ,求和
,求和 (
( );
);
(其中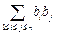 表示所有的积
表示所有的积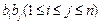 的和)
的和)
(3) 证明: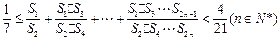 .
.
查看答案和解析>>
科目:高中数学 来源:2010-2011学年重庆市高三5月月考考试理科数学 题型:解答题
本小题满分12分)
古代印度婆罗门教寺庙内的僧侣们曾经玩过一种被称为“河内宝塔问题”的游戏,其玩法如下:如图,设有 个圆盘依其半径大小,大的在下,小的在上套在A杆上,现要将套在A柱上的盘换到C柱上,要求每次只能搬动一个,而且任何不允许将大盘套在小盘上面,假定有三柱子A,B,C可供使用。
个圆盘依其半径大小,大的在下,小的在上套在A杆上,现要将套在A柱上的盘换到C柱上,要求每次只能搬动一个,而且任何不允许将大盘套在小盘上面,假定有三柱子A,B,C可供使用。

现用 表示将n个圆盘全部从A柱上移到C上所至少需要移动的次数,回答下列问题:
表示将n个圆盘全部从A柱上移到C上所至少需要移动的次数,回答下列问题:
(1)写出 ,并求出
,并求出
(2)记 ,求和
,求和 ;
;
(其中 表示所有的积
表示所有的积 的和)
的和)
(3)证明:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com