练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】如图，在直三棱柱中，分别为，的中点，，.

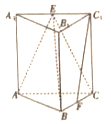
    （1）求证：；

    （2）若直线和平面所成角的正弦值等于，求二面角的正弦值.

    【答案】（1）证明见解析；（2）.

    【解析】

    （1）由线线垂直，证明线面垂直，即平面，再证明

    （2）以点为坐标原点建立空间直角坐标系，求出平面和平面的法向量，通过法向量之间的夹角余弦值，得到二面角的正弦值.

    （1）在直三棱柱中，平面,

    ，

    又，且，平面，，

    ∴平面，又∵平面，

    ∴.

    （2）以点为坐标原点，分别以，，为轴，轴，轴正方向建立空间直角坐标系.

    设，则，，，，，，，，

    直线的方向向量，

    平面的法向量，

    可知，∴，

    ，，，

    设平面的一个法向量，∴取，

    设平面的一个法向量，∴取，

    记二面角的平面角为，，∴，

    ∴二面角的正弦值为.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】为了调查高中生的数学成绩与学生自主学习时间之间的相关关系，新苗中学数学教师对新入学的名学生进行了跟踪调查，其中每周自主做数学题的时间不少于小时的有人，余下的人中，在高三模拟考试中数学成绩不足分的占，统计成绩后，得到如下的列联表：

    分数大于等于分

    分数不足分

    合计

    周做题时间不少于小时

    4

    19

    周做题时间不足小时

    合计

    45

    （）请完成上面的列联表，并判断能否在犯错误的概率不超过的前提下认为“高中生的数学成绩与学生自主学习时间有关”．

    （）（i）按照分层抽样的方法，在上述样本中，从分数大于等于分和分数不足分的两组学生中抽取名学生，设抽到的不足分且周做题时间不足小时的人数为，求的分布列（概率用组合数算式表示）．

    （ii）若将频率视为概率，从全校大于等于分的学生中随机抽取人，求这些人中周做题时间不少于小时的人数的期望和方差．

    附：

    查看答案和解析>>

    科目：高中数学 来源： 题型：

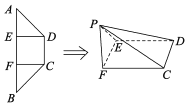
    【题目】如图所示，在等腰梯形ABCD中，，，E，F为AB的三等分点，且将和分别沿DE、CF折起到A、B两点重合，记为点P．

    证明：平面平面PEF；

    若，求PD与平面PFC所成角的正弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在△ABC中,角A,B,C所对的边分别为a,b,c.满足2acosC+bcosC+ccosB=0.

    (Ⅰ)求角C的大小；

    (Ⅱ)若a=2,△ABC的面积为，求C的大小。

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某公司培训员工某项技能，培训有如下两种方式：

    方式一：周一到周五每天培训1小时，周日测试

    方式二：周六一天培训4小时，周日测试

    公司有多个班组，每个班组60人，现任选两组记为甲组、乙组先培训；甲组选方式一，乙组选方式二，并记录每周培训后测试达标的人数如表：

    第一周

    第二周

    第三周

    第四周

    甲组

    20

    25

    10

    5

    乙组

    8

    16

    20

    16

    用方式一与方式二进行培训，分别估计员工受训的平均时间精确到，并据此判断哪种培训方式效率更高？

    在甲乙两组中，从第三周培训后达标的员工中采用分层抽样的方法抽取6人，再从这6人中随机抽取2人，求这2人中至少有1人来自甲组的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知为抛物线：的焦点，过的动直线交抛物线于，两点．当直线与轴垂直时，．

    （1）求抛物线的方程；

    （2）设直线的斜率为1且与抛物线的准线相交于点，抛物线上存在点使得直线，，的斜率成等差数列，求点的坐标．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】“新车嗨翻天!首付3000元起开新车”这就是毛豆新车网打出来的广告语．某人看到广告，兴奋不已，计划于2019年1月在该网站购买一辆某品牌汽车，他从当地了解到近五个月该品牌汽车实际销量如表：

    月份

    2018.08

    2018.09

    2018.10

    2018.11

    2018.12

    月份编号t

    1

    2

    3

    4

    5

    销量y（万辆）

    0.5

    0.6

    1

    1.4

    1.7

    （1）经分析，可用线性回归模型拟合当地该品牌汽车实际销量y（万辆）与月份编号t之间的相关关系．请用最小二乘法求y关于t的线性回归方程，并估计2019年1月份该品牌汽车的销量：

    （2）为了增加销量，厂家和毛豆新车网联合推出对购该品牌车进行补贴．已知某地拟购买该品牌汽车的消费群体十分庞大，某调研机构对其中的200名消费者的购车补贴金额的心理预期值进行了一个抽样调查，得到如下一份频数表：

    补贴金额预期值

    区间（万元）

    [1，2）

    [2，3）

    [3，4）

    [4，5）

    [5，6）

    [6，7）

    频数

    20

    60

    60

    30

    20

    10

    将频率视为概率，现用随机抽样方法从该地区拟购买该品牌汽车的所有消费者中随机抽取3人，记被抽取3人中对补贴金额的心理预期值不低于3万元的人数为ξ，求ξ的分布列及数学期望E（ξ）

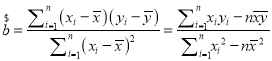    参考公式及数据：①回归方程，其中，；②．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知直线l：与椭圆交于A，B两点，点P是椭圆C上异于A，B的一个动点，点Q在直线AB上，满足(为坐标原点)

    （1）求点Q的轨迹方程；

    （2）求四边形OAPB的面积S的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】光线被曲线反射，等效于被曲线在反射点处的切线反射．已知光线从椭圆的一个焦点出发，被椭圆反射后要回到椭圆的另一个焦点；光线从双曲线的一个焦点出发被双曲线反射后的反射光线等效于从另一个焦点发出；如图，椭圆与双曲线（，）有公共焦点，现一光线从它们的左焦点出发，在椭圆与双曲线间连续反射，则光线经过次反射后，首次回到左焦点所经过的路径长为______．

    查看答案和解析>>

    同步练习册答案