
【题目】已知无穷数列![]() 的各项均为正数,其前
的各项均为正数,其前![]() 项和为
项和为![]() ,
, ![]() .
.
(1)如果![]() ,且对于一切正整数
,且对于一切正整数![]() ,均有
,均有![]() ,求
,求![]() ;
;
(2)如果对于一切正整数![]() ,均有
,均有![]() ,求
,求![]() ;
;
(3)如果对于一切正整数![]() ,均有
,均有![]() ,证明:
,证明: ![]() 能被8整除.
能被8整除.
【答案】(1) ![]() ;(2)
;(2) 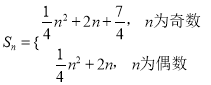 . (3) 见解析.
. (3) 见解析.
【解析】试题分析:(1)由![]() ,得
,得![]() ,根据等比数列的通项公式得到通项;(2)推导出an+1﹣an﹣1=1.a1=4,由anan+1=Sn,得a2=1,a3=5,a4=3,…,由此根据n为偶数和n为奇数,能求出Sn的值;(3)推导出
,根据等比数列的通项公式得到通项;(2)推导出an+1﹣an﹣1=1.a1=4,由anan+1=Sn,得a2=1,a3=5,a4=3,…,由此根据n为偶数和n为奇数,能求出Sn的值;(3)推导出![]() ,分别求出前4项的值,利用数学归纳法能证明a3n﹣1能被8整除.
,分别求出前4项的值,利用数学归纳法能证明a3n﹣1能被8整除.
解析:
(1) 数列![]() 的各项均为正数,由
的各项均为正数,由![]() ,得
,得![]() ,
,
![]() 数列
数列![]() 是等比数列,公比
是等比数列,公比![]() ,从而
,从而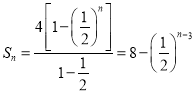
(2) 由![]() 得
得![]() ,两式相减得
,两式相减得![]() ,
,
![]() 此数列各均为正数,
此数列各均为正数, ![]()
![]() ,
, ![]() 数列
数列![]() 和数列
和数列![]() 均是公差为1的等差数列.由
均是公差为1的等差数列.由![]() ,得
,得![]() .
.
当![]() 为偶数时,
为偶数时, ![]()
![]()
当![]() 为奇数时,
为奇数时, ![]()
![]()
 .
.
(3) 由![]() 得
得![]() ,两式相减得
,两式相减得![]() .
.
![]()
![]() ,得
,得![]() ,
, ![]() .
. ![]()
以下证明:对于![]() ,
, ![]() 被8除余数为4,
被8除余数为4, ![]() 被8整除,
被8整除, ![]() 被8除余数为4.
被8除余数为4.
当![]() 时,
时, ![]() ,
, ![]() ,
, ![]() ,命题正确.
,命题正确.
假设![]() 时,命题正确,即
时,命题正确,即![]() ,
, ![]() ,
, ![]() 其中
其中![]() ,
, ![]() .
.
那么, ![]() ,
, ![]()
![]() 为正整数,
为正整数, ![]()
![]() 被8除余数为4.
被8除余数为4.
![]() .
.
![]()
![]() 为正整数,
为正整数, ![]()
![]() 能被8整除.
能被8整除.
![]()
![]() .
. ![]()
![]() 为正整数,
为正整数, ![]()
![]() 被8除余数为4.
被8除余数为4.
即![]() 时,命题也正确.
时,命题也正确.
从而证得,对于一切正整数![]() ,
, ![]() 能被8整除.
能被8整除.


科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,已知直线![]() 与圆O:
与圆O:![]() 相切.
相切.
(1)直线l过点(2,1)且截圆O所得的弦长为![]() ,求直线l的方程;
,求直线l的方程;
(2)已知直线y=3与圆O交于A,B两点,P是圆上异于A,B的任意一点,且直线AP,BP与y轴相交于M,N点.判断点M、N的纵坐标之积是否为定值?若是,求出该定值;若不是,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校高一举行了一次数学竞赛,为了了解本次竞赛学生的成绩情况,从中抽取了部分学生的分数(得分取正整数,满分为![]() )作为样本(样本容量
)作为样本(样本容量![]() )进行统计,按照
)进行统计,按照![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 的分组作出频率分布直方图,已知得分在
的分组作出频率分布直方图,已知得分在![]() 、
、![]() 的频数分别为
的频数分别为![]() 、
、![]() .
.
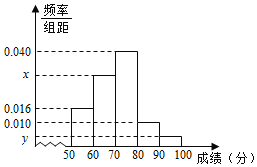
(1)求样本容量![]() 和频率分布直方图中的
和频率分布直方图中的![]() 、
、![]() 的值;
的值;
(2)估计本次竞赛学生成绩的众数、中位数、平均数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学高二年级组织外出参加学业水平考试,出行方式为:乘坐学校定制公交或自行打车前往,大数据分析显示,当![]() 的学生选择自行打车,自行打车的平均时间为
的学生选择自行打车,自行打车的平均时间为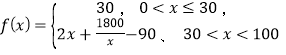 (单位:分钟) ,而乘坐定制公交的平均时间不受
(单位:分钟) ,而乘坐定制公交的平均时间不受![]() 影响,恒为40分钟,试根据上述分析结果回答下列问题:
影响,恒为40分钟,试根据上述分析结果回答下列问题:
(1)当![]() 在什么范围内时,乘坐定制公交的平均时间少于自行打车的平均时间?
在什么范围内时,乘坐定制公交的平均时间少于自行打车的平均时间?
(2)求该校学生参加考试平均时间![]() 的表达式:讨论
的表达式:讨论![]() 的单调性,并说明其实际意义.
的单调性,并说明其实际意义.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某动物园要为刚入园的小动物建造一间两面靠墙的三角形露天活动室,地面形状如图所示,已知已有两面墙的夹角为![]() ,墙
,墙![]() 的长度为
的长度为![]() 米,(已有两面墙的可利用长度足够大),记
米,(已有两面墙的可利用长度足够大),记![]() .
.
(1)若![]() ,求
,求![]() 的周长(结果精确到0.01米);
的周长(结果精确到0.01米);
(2)为了使小动物能健康成长,要求所建的三角形露天活动室面积,![]() 的面积尽可能大,当
的面积尽可能大,当![]() 为何值时,该活动室面积最大?并求出最大面积.
为何值时,该活动室面积最大?并求出最大面积.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校从参加高三模拟考试的学生中随机抽取60名学生,将其数学成绩(均为整数)分成六组[90,100),[100,110),…,[140,150]后得到如下部分频率分布直方图,观察图形的信息,回答下列问题:
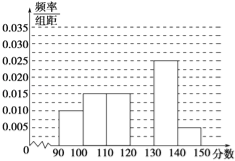
(1)求分数在[120,130)内的频率;
(2)若在同一组数据中,将该组区间的中点值(如:组区间[100,110)的中点值为![]() =105)作为这组数据的平均分,据此,估计本次考试的平均分;
=105)作为这组数据的平均分,据此,估计本次考试的平均分;
(3)用分层抽样的方法在分数段为[110,130)的学生中抽取一个容量为6的样本,将该样本看成一个总体,从中任取2人,求至多有1人在分数段[120,130)内的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,动点
中,动点![]() 到定点
到定点![]() 的距离与它到直线
的距离与它到直线![]() 的距离相等.
的距离相等.
(1)求动点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)设动直线![]() 与曲线
与曲线![]() 相切于点
相切于点![]() ,与直线
,与直线![]() 相交于点
相交于点![]() .
.
证明:以![]() 为直径的圆恒过
为直径的圆恒过![]() 轴上某定点.
轴上某定点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆M:![]() ,直线l:
,直线l:![]() ,下列四个选项,其中正确的是( )
,下列四个选项,其中正确的是( )
A.对任意实数k与θ,直线l和圆M有公共点
B.存在实数k与θ,直线l和圆M相离
C.对任意实数k,必存在实数θ,使得直线l与圆M相切
D.对任意实数θ,必存在实数k,使得直线l与圆M相切
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com