
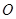 的直线
的直线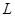 与抛物线
与抛物线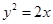 相交于
相交于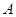 、
、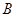 两点,且
两点,且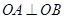 ,
,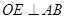 于
于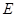 .
.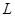 过定点;
过定点; 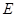 的轨迹方程.
的轨迹方程.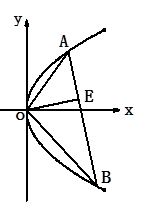
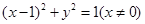 .
.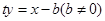 ,然后根据题目给的方程条件
,然后根据题目给的方程条件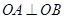 ,即可确定b的值或找到b与t的关系,进而确定定点.
,即可确定b的值或找到b与t的关系,进而确定定点.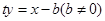 与抛物线
与抛物线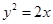 相交于
相交于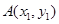 、
、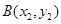 两点
两点 ……………………2分
……………………2分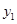 、
、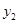 是此方程的两实根,由韦达定理得:
是此方程的两实根,由韦达定理得: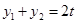
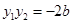 ……………………3分
……………………3分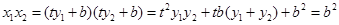 …………4分
…………4分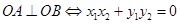 ……………………5分
……………………5分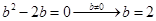 ……………………6分
……………………6分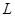 :
: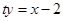 过定点
过定点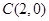 ……………………8分
……………………8分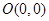 ,
,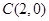 ,
,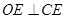 ……………………9分
……………………9分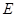 的轨迹是以线段
的轨迹是以线段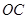 为直径的圆除去点
为直径的圆除去点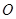 , ……………………11分
, ……………………11分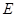 的轨迹方程为
的轨迹方程为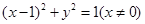 ……………………12分
……………………12分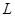 的方程设为
的方程设为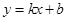 又没有讨论
又没有讨论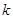 不存在的情况扣2分;轨迹方程中没有限制
不存在的情况扣2分;轨迹方程中没有限制 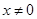 扣1分.
扣1分.

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com