函数f(x)=x3+ax2+bx+c,曲线y=f(x)在点(1,f(1))处的切线平行于直线y=3x+1,若函数y=f(x)在x=-2时有极值.
(1)求a,b的值;
(2)求函数f(x)的单调区间;
(3)若函数f(x)在区间[-3,1]上的最大值为10,求f(x)在该区间上的最小值.
【答案】
分析:(1)切点在切线上求出点P的坐标,然后根据曲线上过点P(1,f(1)) 的切线方程为y=3x+1,且函数y=f(x)在x=-2 时有极值得f'(1)=3,f'(-2)=0,建立不等式组,解之即可求出a,b的值;.
(2)先求出其导函数,根据导函数值大于0以及小于0即可求出函数f(x)的单调区间;
(3)先分析出何时取最大值,结合最大值为10求出c,再结合函数值即可得到f(x)在该区间上的最小值.
解答:解:(1)由题意知P(1,4),
f′(x)=3x
2+2ax+b …(2分)
∵曲线上过点P(1,f(1)) 的切线方程平行与y=3x+1,且函数y=f(x)在x=-2 时有极值.
∴
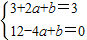
,解得
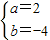
.
∴f(x)=x
3+2x
2-4x+c
(2)∵f'(x)=3x
2+4x-4=(3x-2)(x+2)
∴x>

,x<-2,f'(x)>0;
-2<x<

,f'(x)<0.
∴函数f(x)的单调增区间为:(-∞,-2)(

,+∞)
单调减区间为:(-2,

)
(3)∵函数在[-3,-2)上增,(-2,

)上减,(

,1]上增;
且f(-2)=8+c,f(1)=-1+c;f(-3)=3+c,f(

)=-
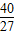
+c;
由函数f(x)在区间[-3,1]上的最大值为10,
得f(-2)=8+c=10⇒c=2,
∴f(x)在该区间上的最小值为:
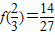
.
点评:本题考查导数的几何意义:导数在切点处的值是切线的斜率;考查函数单调递增对应的导函数大于等于0恒成立.

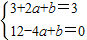 ,解得
,解得 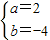 .
. ,x<-2,f'(x)>0;
,x<-2,f'(x)>0; ,f'(x)<0.
,f'(x)<0. ,+∞)
,+∞) )
) )上减,(
)上减,( ,1]上增;
,1]上增; )=-
)=-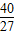 +c;
+c;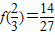 .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案