Question

正方体中不在同一表面上两顶点坐标为M（-1，2，-1），N（3，-2，3），则此正方体的内切球的表面积为    ．

Answer 1

【答案】分析：先根据题意可知MN是正方体的题对角线，利用空间两点的距离公式求出MN，再根据正方体的棱长是内切球的直接求出半径，最后根据球的表面积公式进行求解即可．
解答：解：∵正方体中不在同一表面上两顶点坐标为M（-1，2，-1），N（3，-2，3），
∴MN是正方体的题对角线，MN==
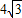
∴正方体的棱长为4，正方体的内切球的半径为2
∴正方体的内切球的表面积为16π
故答案为：16π
点评：本题主要考查了空间两点的距离公式，以及正方体的内切球的有关知识，属于基础题．