【题目】p：方程x2+2mx+1＝0有两个不相等的正根，q：不等式m2﹣m﹣6＜0成立；求使p∨q为真，p∧q为假时，实数m的取值范围．
【答案】（﹣∞，﹣2]∪[﹣1，1]∪[3，+∞）
【解析】
由p：方程x2+2mx+1＝0有两个不相等的正根，解出m的取值范围，由q：不等式m2﹣m﹣6＜0成立，解出m的取值范围，再由p∨q为真，p∧q为假，可知p与q一真一假，由此可解得m的取值范围．
p：方程x2+2mx+1＝0有两个不相等的正根，则△＝4m2﹣4＞0，解得m＞1或m＜﹣1；
q：不等式m2﹣m﹣6＜0成立，则﹣2＜m＜3，
若p∨q为真，p∧q为假时，则命题p与命题q一真一假，
当p真q假时，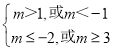
，解得m≤﹣2或m≥3，
当q真p假时，
，解得﹣1≤m≤1，
综上，实数m的取值范围（﹣∞，﹣2]∪[﹣1，1]∪[3，+∞）．
步步高口算题卡系列答案
点睛新教材全能解读系列答案
小学教材完全解读系列答案科目：高中数学 来源： 题型：
【题目】已知双曲线
过点
且渐近线为
，则下列结论正确的个数为（ ）
①的实轴长为
；②的离心率为
；
③曲线
经过的一个焦点；④直线
与有两个公共点.
A.
个B.
个C.
个D.
个
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】图1是由矩形
和菱形
组成的一个平面图形，其中
， 
，将其沿
折起使得
与
重合，连结
，如图2.
（1）证明图2中的
四点共面，且平面
平面
；
（2）求图2中的四边形
的面积.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，在三棱柱ABC-
中，
平面ABC，D，E，F，G分别为
，AC，
，
的中点，AB=BC=
，AC==2．
（Ⅰ）求证：AC⊥平面BEF；
（Ⅱ）求二面角B-CD-C1的余弦值；
（Ⅲ）证明：直线FG与平面BCD相交．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】设三棱锥
的底面是正三角形，侧棱长均相等，
是棱
上的点（不含端点），记直线
与直线
所成角为
，直线与平面
所成角为
，二面角
的平面角为
，则（ ）
A. 
B. 
C. 
D. 
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，在△MBC中，MA是BC边上的高，MA＝3，AC＝4，将△MBC沿MA进行翻折，使得∠BAC＝90°如图，再过点B作BD∥AC，连接AD，CD，MD且
，∠CAD＝30°．
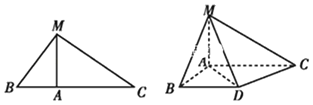
（1）求证：平面MCD⊥平面MAD；
（2）求点B到平面MAD的距离．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知椭圆
的焦距为
，且过点
．
（1）求椭圆的方程；
（2）已知
，是否存在
使得点
关于
的对称点
（不同于点）在椭圆
上？若存在求出此时直线的方程，若不存在说明理由．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
