Question

【题目】某食品厂为了检查甲、乙两条自动包装流水线的生产情况，随机在这两条流水线上各抽取40件产品作为样本，并称出它们的重量(单位：克)，重量值落在[495，510)内的产品为合格品，否则为不合格品．统计结果如下：

甲流水线样本的频数分布表

产品重量(克)	频数
[490，495)	6
[495，500)	8
[500，505)	14
[505，510)	8
[510，515]	4

乙流水线样本的频率分布直方图

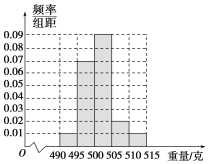
(1)求甲流水线样本合格的频率；

(2)由以上统计数据完成下面2×2列联表，并回答有多大的把握认为产品的包装质量与两条自动包装流水线的选择有关．

分类	甲流水线	乙流水线	总计
合格品
不合格品
总计

附：K2＝.

P(K2≥k0)	0.15	0.10	0.05	0.025	0.010	0.005	0.001
k0	2.072	2.706	3.841	5.024	6.635	7.879	10.828

Answer 1

【答案】（1） ； （2）有的把握认为产品的包装质量与两条自动包装流水线的选择有关.

【解析】

（1）利用频率分布直方图计算样本合格的频率；(2)完善2×2列联表，代入公式求解．

(1)由表知甲流水线样本中合格品数为8＋14＋8＝30，故甲流水线样本中合格品的频率为＝0.75.

(2)由(1)知甲流水线样本中合格品格数30，乙流水线样本中合格品数为0.9×40＝36.

则2×2列联表如下：

分类	甲流水线	乙流水线	总计
合格品	30	36	66
不合格品	10	4	14
总计	40	40	80

由2×2列联表中的数据得K2的观测值为

K＝≈3.12>2.706.

故有90%的把握认为产品的包装质量与两条自动包装流水线的选择有关．