
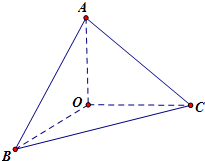
 如图所示,三棱锥O-ABC中,OA=OB=OC=2,且,OA、OB、OC两两垂直(每两条都垂直).
如图所示,三棱锥O-ABC中,OA=OB=OC=2,且,OA、OB、OC两两垂直(每两条都垂直). 解(1)VO-ABC=VA-OBC=
解(1)VO-ABC=VA-OBC=| 1 |
| 3 |
| 4 |
| 3 |
| 2 |
| 3 |
| 1 |
| 3 |
| 4 |
| 3 |
| 2 |
| 3 |
| 3 |
| 2 |
| 3 |
| 3 |
| 3 |
| 3 |


科目:高中数学 来源: 题型:
 已知正方形ABCD的边长为2
已知正方形ABCD的边长为2| 2 |
查看答案和解析>>
科目:高中数学 来源:2012-2013学年福建省漳州市七校高三第三次联考理科数学试卷(解析版) 题型:填空题
如图所示是三棱锥D—ABC的三视图,若在三棱锥的直观图中,点O为线段BC的中点,则异面直线DO与AB所成角的余弦值等于______。
查看答案和解析>>
科目:高中数学 来源:2012-2013学年正大学校高三(上)周练数学试卷(15)(理科)(解析版) 题型:选择题
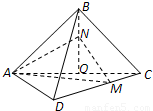 已知正方形ABCD的边长为2
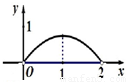
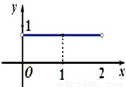
已知正方形ABCD的边长为2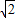 ,将△ABC沿对角线AC折起,使平面ABC⊥平面ACD,得到如图所示的三棱锥B-ACD.若O为AC边的中点,M,N分别为线段DC,BO上的动点(不包括端点),且BN=CM.设BN=x,则三棱锥N-AMC的体积y=f(x)的函数图象大致是( )
,将△ABC沿对角线AC折起,使平面ABC⊥平面ACD,得到如图所示的三棱锥B-ACD.若O为AC边的中点,M,N分别为线段DC,BO上的动点(不包括端点),且BN=CM.设BN=x,则三棱锥N-AMC的体积y=f(x)的函数图象大致是( )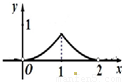

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com