
【题目】求函数y=( ![]() )x﹣(
)x﹣( ![]() )x+1,x∈[﹣3,2]的单调区间,并求它的值域.
)x+1,x∈[﹣3,2]的单调区间,并求它的值域.
【答案】解:∵y= ![]() ﹣(
﹣( ![]() )x+1,∴令t=
)x+1,∴令t= ![]() ,∵x∈[﹣3,2],∴t∈[
,∵x∈[﹣3,2],∴t∈[ ![]() ,8]∴原函数可化为y=t2﹣t+1=(t﹣
,8]∴原函数可化为y=t2﹣t+1=(t﹣ ![]() )2+
)2+ ![]() ,(t∈[
,(t∈[ ![]() ,8],)∴t=
,8],)∴t= ![]() 是对称轴
是对称轴
∵x∈[﹣3,1]时,x增大t= ![]() 递减,且t∈[
递减,且t∈[ ![]() ,8],y=(t﹣
,8],y=(t﹣ ![]() )2+
)2+ ![]() 递减
递减
∴[﹣3,1]是函数y=( ![]() )x﹣(
)x﹣( ![]() )x+1的递减区间,同理,[1,2]是函数的递增区间
)x+1的递减区间,同理,[1,2]是函数的递增区间
∴ymin= ![]() ,ymax=57
,ymax=57
故原函数递减区间是[﹣3,1],递增区间是[1,2],值域是[ ![]() ,57]
,57]
【解析】令t= ![]() ,将原函数化为二次函数y=t2﹣t+1,再根据复合函数的性质即可
,将原函数化为二次函数y=t2﹣t+1,再根据复合函数的性质即可
【考点精析】认真审题,首先需要了解复合函数单调性的判断方法(复合函数f[g(x)]的单调性与构成它的函数u=g(x),y=f(u)的单调性密切相关,其规律:“同增异减”).


科目:高中数学 来源: 题型:
【题目】设α是空间中的一个平面,l,m,n是三条不同的直线,则下列命题中正确的是( )
A.若mα,nα,l⊥m,l⊥n,则l⊥α
B.若mα,n⊥α,l⊥n,则l∥m
C.若l∥m,m⊥α,n⊥α,则l∥n
D.若l⊥m,l⊥n,则n∥m
查看答案和解析>>
科目:高中数学 来源: 题型:
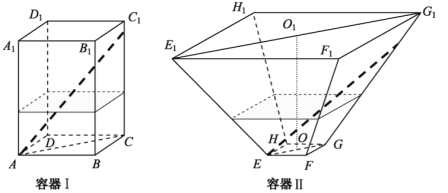
【题目】如图,水平放置的正四棱柱形玻璃容器Ⅰ和正四棱台形玻璃容器Ⅱ的高均为32cm,容器Ⅰ的底面对角线AC的长为10![]() cm,容器Ⅱ的两底面对角线
cm,容器Ⅱ的两底面对角线![]() ,
,![]() 的长分别为14cm和62cm.分别在容器Ⅰ和容器Ⅱ中注入水,水深均为12cm.现有一根玻璃棒l,其长度为40cm.(容器厚度、玻璃棒粗细均忽略不计)
的长分别为14cm和62cm.分别在容器Ⅰ和容器Ⅱ中注入水,水深均为12cm.现有一根玻璃棒l,其长度为40cm.(容器厚度、玻璃棒粗细均忽略不计)
(1)将![]() 放在容器Ⅰ中,
放在容器Ⅰ中,![]() 的一端置于点A处,另一端置于侧棱
的一端置于点A处,另一端置于侧棱![]() 上,求
上,求![]() 没入水中部分的长度;
没入水中部分的长度;
(2)将![]() 放在容器Ⅱ中,
放在容器Ⅱ中,![]() 的一端置于点E处,另一端置于侧棱
的一端置于点E处,另一端置于侧棱![]() 上,求
上,求![]() 没入水中部分的长度.
没入水中部分的长度.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,O为等腰三角形ABC内一点,⊙O与△ABC的底边BC交于M,N两点,与底边上的高AD交于点G,且与AB,AC分别相切于E,F两点. 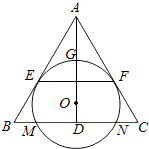
(1)证明:EF∥BC;
(2)若AG等于⊙O的半径,且AE=MN=2 ![]() ,求四边形EBCF的面积.
,求四边形EBCF的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】
已知函数![]() ,
,![]() .
.
(1)若曲线![]() 在点
在点![]() 处的切线与直线
处的切线与直线![]() 垂直,求
垂直,求![]() 的值;
的值;
(2)若![]() 存在极小值
存在极小值![]() 时,不等式
时,不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
(3)当![]() 时,如果存在两个不相等的正数
时,如果存在两个不相等的正数![]() ,使得
,使得![]() ,求证:
,求证:![]() .
.
请考生在第22、23两题中任选一题作答.注意:只能做所选定的题目.如果多做,则按所做的第一个题目计分.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2﹣2|x|﹣3a
(1)当a=1时,在所给坐标系中,画出函数f(x)的图象,并求f(x)的单调递增区间
(2)若直线y=1与函数f(x)的图象有4个交点,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合A={x|2x2+ax+2=0,a∈R},B={x|x2+3x+2a=0,a∈R},A∩B={2}且A∪B=I,则(IA)∪(IB)=( )
A.{﹣5, ![]() }
}
B.{﹣5, ![]() ,2}
,2}
C.{﹣5,2}
D.{ ![]() ,2}
,2}
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 与
与![]() 的定义域为
的定义域为![]() ,有下列5个命题:
,有下列5个命题:
①若![]() ,则
,则![]() 的图象自身关于直线
的图象自身关于直线![]() 轴对称;
轴对称;
②![]() 与
与![]() 的图象关于直线
的图象关于直线![]() 对称;
对称;
③函数![]() 与
与![]() 的图象关于
的图象关于![]() 轴对称;
轴对称;
④![]() 为奇函数,且
为奇函数,且![]() 图象关于直线
图象关于直线![]() 对称,则
对称,则![]() 周期为2;
周期为2;
⑤![]() 为偶函数,
为偶函数, ![]() 为奇函数,且
为奇函数,且![]() ,则
,则![]() 周期为2.
周期为2.
其中正确命题的序号是____________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com