Question

如下图,直线l₁和l₂相交于M,且l₁⊥l₂,点N∈l₁.已知以A、B为端点的曲线段C上任一点到l₂的距离与到N的距离相等.若△AMN为锐角三角形,|AM|=,|AN|=3,且|BN|=6,建立适当的坐标系,求曲线段C的方程.

Answer 1

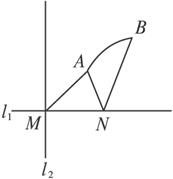
思路分析:求轨迹方程旨在合理地建系、设点.根据题设或相关的定义找出问题的内在联系,进而求得曲线方程.

解:根据抛物线的定义,可将l₁取为x轴、MN的中垂线为y轴建立直角坐标系.

这样曲线段C的方程可设为y²=2px.

于是可设A(x₁,y₁)、B(x₂,y₂),则M(-,0),N(,0),C:y²=2px(x₁≤x≤x₂,y＞0).

由条件得

即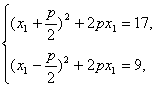

解得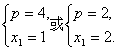

又由△AMN是锐角三角形,

∴＞x₁(结合图形).

因此p=4,x₁=1,

∴C的方程为y²=8x.

而|BN|=6,

∴(x₂-)²+y₂²=36,

即(x₂-2)²+8x₂=36,解得x₂=4.

故所求的曲线段C的方程为y²=8x(1≤x≤4,y＞0).