
【题目】在直角坐标系xoy中,曲线C1上的点均在C2:(x﹣5)2+y2=9外,且对C1上任意一点M,M到直线x=﹣2的距离等于该点与圆C2上点的距离的最小值.
(1)求曲线C1的方程
(2)设P(x0 , y0)(y0≠±3)为圆C2外一点,过P作圆C2的两条切线,分别于曲线C1相交于点A,B和C,D.证明:当P在直线x=﹣4上运动时,四点A,B,C,D的纵坐标之积为定值.
【答案】
(1)
解:设M的坐标为(x,y),由已知得|x+2|= ![]() 且圆C2上的点位于直线x=﹣2的右侧
且圆C2上的点位于直线x=﹣2的右侧
∴ ![]() =x+5
=x+5
化简得曲线C1的方程为y2=20x
(2)
证明:当点P在直线x=﹣4上运动时,P的坐标为(﹣4,y0),
∵y0≠±3,∴过P且与圆C2相切的直线的斜率k存在且不为0,每条切线都与抛物线有两个交点,切线方程为
y﹣y0=k(x+4),即kx﹣y+y0+4k=0,
∴ ![]() ,整理得
,整理得 ![]() ①
①
设过P所作的两条切线PA,PC的斜率分别为k1,k2,则k1,k2是方程①的两个实根
∴ ![]() ②
②
由 ![]() ,消元可得
,消元可得 ![]() ③
③
设四点A,B,C,D的纵坐标分别为y1,y2,y3,y4,
∴y1,y2是方程③的两个实根
∴ ![]() ④
④
同理可得 ![]() ⑤
⑤
由①②④⑤可得 ![]() =
= ![]() =6400
=6400
∴当P在直线x=﹣4上运动时,四点A,B,C,D的纵坐标之积为定值为6400.
【解析】(1)设M的坐标为(x,y),根据对C1上任意一点M,M到直线x=﹣2的距离等于该点与圆C2上点的距离的最小值,可得|x+2|= ![]() 且圆C2上的点位于直线x=﹣2的右侧,从而可得曲线C1的方程;(2)当点P在直线x=﹣4上运动时,P的坐标为(﹣4,y0),设切线方程为kx﹣y+y0+4k=0,利用直线与圆相切可得
且圆C2上的点位于直线x=﹣2的右侧,从而可得曲线C1的方程;(2)当点P在直线x=﹣4上运动时,P的坐标为(﹣4,y0),设切线方程为kx﹣y+y0+4k=0,利用直线与圆相切可得 ![]() ,从而可得过P所作的两条切线PA,PC的斜率k1 , k2是方程的两个实根,设四点A,B,C,D的纵坐标分别为y1 , y2 , y3 , y4 , 从而可得
,从而可得过P所作的两条切线PA,PC的斜率k1 , k2是方程的两个实根,设四点A,B,C,D的纵坐标分别为y1 , y2 , y3 , y4 , 从而可得 ![]() ;同理可得
;同理可得 ![]() ,由此可得当P在直线x=﹣4上运动时,四点A,B,C,D的纵坐标之积为定值为6400.
,由此可得当P在直线x=﹣4上运动时,四点A,B,C,D的纵坐标之积为定值为6400.


 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和Sn=﹣ ![]() n2+kn(其中k∈N+),且Sn的最大值为8.
n2+kn(其中k∈N+),且Sn的最大值为8.
(1)确定常数k,求an;
(2)求数列 ![]() 的前n项和Tn .
的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】
(1)[选修4﹣1:几何证明选讲]
如图,AB是圆O的直径,D,E为圆上位于AB异侧的两点,连接BD并延长至点C,使BD=DC,连接AC,AE,DE.
求证:∠E=∠C.
(2)[选修4﹣2:矩阵与变换]
已知矩阵A的逆矩阵  ,求矩阵A的特征值.
,求矩阵A的特征值.
(3)[选修4﹣4:坐标系与参数方程]
在极坐标中,已知圆C经过点P( ![]() ,
, ![]() ),圆心为直线ρsin(θ﹣
),圆心为直线ρsin(θ﹣ ![]() )=﹣
)=﹣ ![]() 与极轴的交点,求圆C的极坐标方程.
与极轴的交点,求圆C的极坐标方程.
(4)[选修4﹣5:不等式选讲]
已知实数x,y满足:|x+y|< ![]() ,|2x﹣y|<
,|2x﹣y|< ![]() ,求证:|y|<
,求证:|y|< ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点A(﹣1,0),B(1,0),C(0,1),直线y=ax+b(a>0)将△ABC分割为面积相等的两部分,则b的取值范围是( )
A.(0,1)B. C.
C. D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,以坐标原点为极点,
中,以坐标原点为极点,![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]()
![]() ,过点
,过点![]() 的直线
的直线![]() 的参数方程为
的参数方程为 (
(![]() 为参数),
为参数),![]() 与
与![]() 交于
交于![]() 两点
两点
(1) 求![]() 的直角坐标方程和
的直角坐标方程和![]() 的普通方程;
的普通方程;
(2) 若![]() ,
,![]() ,
,![]() 成等比数列,求
成等比数列,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,则
,则![]() _____.
_____.
【答案】![]()
【解析】
分子分母同时除以![]() ,把目标式转为
,把目标式转为![]() 的表达式,代入可求.
的表达式,代入可求.
![]() ,则
,则![]()
![]()
故答案为:![]() .
.
【点睛】
本题考查三角函数的化简求值,常用方法:(1)弦切互化法:主要利用公式![]() , 形如
, 形如![]() 等类型可进行弦化切;(2)“1”的灵活代换
等类型可进行弦化切;(2)“1”的灵活代换![]() 和
和![]() 的关系进行变形、转化.
的关系进行变形、转化.
【题型】填空题
【结束】
15
【题目】如图,正方体![]() 的棱长为1,
的棱长为1,![]() 为
为![]() 中点,连接
中点,连接![]() ,则异面直线
,则异面直线![]() 和
和![]() 所成角的余弦值为_____.
所成角的余弦值为_____.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】北京某附属中学为了改善学生的住宿条件,决定在学校附近修建学生宿舍,学校总务办公室用1000万元从政府购得一块廉价土地,该土地可以建造每层1000平方米的楼房,楼房的每平方米建筑费用与建筑高度有关,楼房每升高一层,整层楼每平方米建筑费用提高0.02万元,已知建筑第5层楼房时,每平方米建筑费用为0.8万元.
(1)若学生宿舍建筑为![]() 层楼时,该楼房综合费用为
层楼时,该楼房综合费用为![]() 万元,综合费用是建筑费用与购地费用之和),写出
万元,综合费用是建筑费用与购地费用之和),写出![]() 的表达式;
的表达式;
(2)为了使该楼房每平方米的平均综合费用最低,学校应把楼层建成几层?此时平均综合费用为每平方米多少万元?
【答案】(1)![]() ;(2)学校应把楼层建成
;(2)学校应把楼层建成![]() 层,此时平均综合费用为每平方米
层,此时平均综合费用为每平方米![]() 万元
万元
【解析】
![]() 由已知求出第
由已知求出第![]() 层楼房每平方米建筑费用为
层楼房每平方米建筑费用为![]() 万元,得到第
万元,得到第![]() 层楼房建筑费用,由楼房每升高一层,整层楼建筑费用提高
层楼房建筑费用,由楼房每升高一层,整层楼建筑费用提高![]() 万元
万元![]() ,然后利用等差数列前
,然后利用等差数列前![]() 项和求建筑
项和求建筑![]() 层楼时的综合费用
层楼时的综合费用![]() ;
;
![]() 设楼房每平方米的平均综合费用为
设楼房每平方米的平均综合费用为![]() ,则
,则![]() ,然后利用基本不等式求最值.
,然后利用基本不等式求最值.
解:![]() 由建筑第5层楼房时,每平方米建筑费用为
由建筑第5层楼房时,每平方米建筑费用为![]() 万元,
万元,
且楼房每升高一层,整层楼每平方米建筑费用提高![]() 万元,
万元,
可得建筑第1层楼房每平方米建筑费用为:![]() 万元.
万元.
建筑第1层楼房建筑费用为:![]() 万元
万元![]() .
.
楼房每升高一层,整层楼建筑费用提高:![]() 万元
万元![]() .
.
建筑第x层楼时,该楼房综合费用为:![]() .
.
![]() ;
;
![]() 设该楼房每平方米的平均综合费用为
设该楼房每平方米的平均综合费用为![]() ,
,
则:![]() ,
,
当且仅当![]() ,即
,即![]() 时,上式等号成立.
时,上式等号成立.
![]() 学校应把楼层建成10层,此时平均综合费用为每平方米
学校应把楼层建成10层,此时平均综合费用为每平方米![]() 万元.
万元.
【点睛】
本题考查简单的数学建模思想方法,训练了等差数列前n项和的求法,训练了利用基本不等式求最值,是中档题.
【题型】解答题
【结束】
20
【题目】已知![]() .
.
(1)求函数![]() 的最小正周期和对称轴方程;
的最小正周期和对称轴方程;
(2)若![]() ,求
,求![]() 的值域.
的值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现有0,1,2,3,4,5六个数字.
(1)用所给数字能够组成多少个四位数?
(2)用所给数字可以组成多少个没有重复数字的五位数?
(3)用所给数字可以组成多少个没有重复数字且比3142大的数?(最后结果均用数字作答)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知四棱锥P - ABCD的底面为直角梯形,AB∥DC,∠DAB=90°,PA⊥底面ABCD,且PA=AD=DC![]()
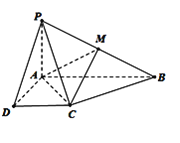
(1)证明平面PAD⊥平面PCD;
(2)求AC与PB所成角的余弦值;
(3)求平面AMC与平面BMC所成二面角的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com