
已知抛物线C: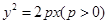 的焦点为F,直线
的焦点为F,直线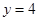 与y轴的交点为P,与C的交点为Q,且
与y轴的交点为P,与C的交点为Q,且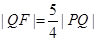 .
.
(1)求C的方程;
(2)过F的直线 与C相交于A,B两点,若AB的垂直平分线
与C相交于A,B两点,若AB的垂直平分线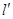 与C相较于M,N两点,且A,M,B,N四点在同一圆上,求
与C相较于M,N两点,且A,M,B,N四点在同一圆上,求 的方程.
的方程.
(1)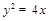 ;(2)直线
;(2)直线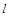 的方程为
的方程为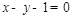 或
或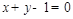 .
.
解析试题分析:(1)由已知条件,先求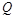 点的坐标,再由
点的坐标,再由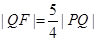 及抛物线的焦半径公式列方程可求得
及抛物线的焦半径公式列方程可求得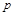 的值,从而可得抛物线C的方程;(2)由已知条件可知直线
的值,从而可得抛物线C的方程;(2)由已知条件可知直线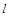 与坐标轴不垂直,故可设直线
与坐标轴不垂直,故可设直线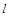 的点参式方程:
的点参式方程: ,代入
,代入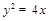 消元得
消元得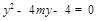 .设
.设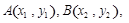 由韦达定理及弦长公式表示
由韦达定理及弦长公式表示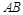 的中点
的中点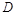 的坐标及
的坐标及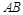 长,同理可得
长,同理可得 的中点
的中点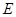 的坐标及
的坐标及 的长.由于
的长.由于 垂直平分线
垂直平分线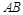 ,故
,故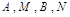 四点在同一圆上等价于
四点在同一圆上等价于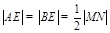 ,由此列方程可求得
,由此列方程可求得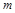 的值,进而可得直线
的值,进而可得直线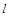 的方程.
的方程.
试题解析:(1)设 ,代入
,代入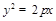 ,得
,得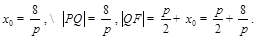 .由题设得
.由题设得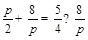 ,解得
,解得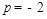 (舍去)或
(舍去)或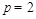 ,∴C的方程为
,∴C的方程为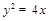 ;(2)由题设知
;(2)由题设知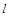 与坐标轴不垂直,故可设
与坐标轴不垂直,故可设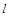 的方程为
的方程为 ,代入
,代入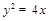 得
得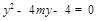 .设
.设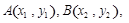 则
则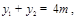
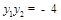 .故
.故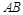 的中点为
的中点为 .又
.又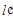 的斜率为
的斜率为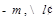 的方程为
的方程为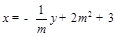 .将上式代入
.将上式代入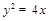 ,并整理得
,并整理得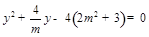 .设
.设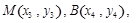 则
则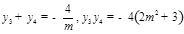 .故
.故 的中点为
的中点为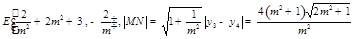 .
.
由于 垂直平分线
垂直平分线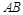 ,故
,故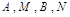 四点在同一圆上等价于
四点在同一圆上等价于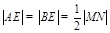 ,从而
,从而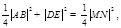 即
即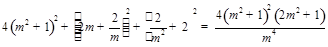 ,化简得
,化简得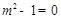 ,解得
,解得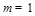 或
或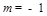 .所求直线
.所求直线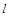 的方程为
的方程为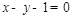 或
或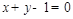 .
.
考点:1.抛物线的几何性质;2.抛物线方程的求法;3.直线与抛物线的位置关系.


科目:高中数学 来源: 题型:解答题
已知点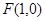 ,直线
,直线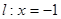 ,动点P到点F的距离与到直线
,动点P到点F的距离与到直线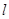 的距离相等.
的距离相等.
(1)求动点P的轨迹C的方程;
(2)直线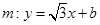 与曲线C交于A,B两点,若曲线C上存在点D使得四边形FABD为平行四边形,求b的值.
与曲线C交于A,B两点,若曲线C上存在点D使得四边形FABD为平行四边形,求b的值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图5, 为坐标原点,双曲线
为坐标原点,双曲线 和椭圆
和椭圆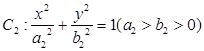 均过点
均过点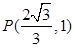 ,且以
,且以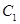 的两个顶点和
的两个顶点和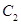 的两个焦点为顶点的四边形是面积为2的正方形.
的两个焦点为顶点的四边形是面积为2的正方形.
(1)求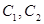 的方程;
的方程;
(2)是否存在直线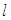 ,使得
,使得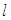 与
与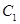 交于
交于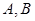 两点,与
两点,与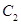 只有一个公共点,且
只有一个公共点,且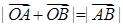 ?证明你的结论.
?证明你的结论.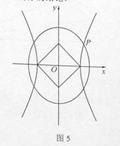
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,已知椭圆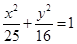 的右焦点为
的右焦点为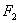 ,点
,点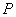 是椭圆上任意一点,圆
是椭圆上任意一点,圆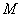 是以
是以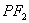 为直径的圆.
为直径的圆.
(1)若圆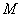 过原点
过原点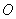 ,求圆
,求圆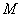 的方程;
的方程;
(2)写出一个定圆的方程,使得无论点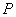 在椭圆的什么位置,该定圆总与圆
在椭圆的什么位置,该定圆总与圆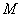 相切,请写出你的探究过程.
相切,请写出你的探究过程. 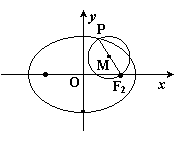
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
在平面直角坐标系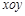 中,已知椭圆的焦点在
中,已知椭圆的焦点在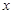 轴上,离心率为
轴上,离心率为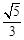 ,且经过点
,且经过点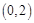 .
.
(1)求椭圆的标准方程;
(2) 以椭圆的长轴为直径作圆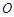 ,设
,设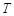 为圆
为圆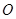 上不在坐标轴上的任意一点,
上不在坐标轴上的任意一点, 为
为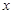 轴上一点,过圆心
轴上一点,过圆心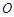 作直线
作直线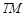 的垂线交椭圆右准线于点
的垂线交椭圆右准线于点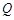 .问:直线
.问:直线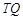 能否与圆
能否与圆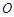 总相切,如果能,求出点
总相切,如果能,求出点 的坐标;如果不能,说明理由.
的坐标;如果不能,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知双曲线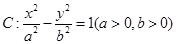 的两个焦点为
的两个焦点为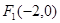 、
、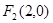 点
点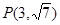 在双曲线C上.
在双曲线C上.
(1)求双曲线C的方程;
(2)记O为坐标原点,过点Q (0,2)的直线l与双曲线C相交于不同的两点E、F,若△OEF的面积为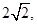 求直线l的方程.
求直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
在平面直角坐标系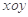 中,已知椭圆
中,已知椭圆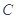 ∶
∶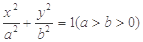 的左、右焦点分别
的左、右焦点分别 、
、 焦距为
焦距为 ,且与双曲线
,且与双曲线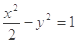 共顶点.
共顶点.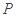 为椭圆
为椭圆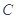 上一点,直线
上一点,直线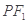 交椭圆
交椭圆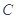 于另一点
于另一点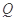 .
.
(1)求椭圆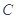 的方程;
的方程;
(2)若点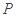 的坐标为
的坐标为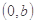 ,求过
,求过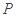 、
、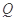 、
、 三点的圆的方程;
三点的圆的方程;
(3)若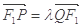 ,且
,且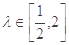 ,求
,求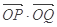 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知椭圆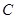 的中心在原点,焦点在
的中心在原点,焦点在 轴上,离心率为
轴上,离心率为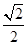 ,它的一个焦点恰好与抛物线
,它的一个焦点恰好与抛物线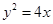 的焦点重合.
的焦点重合.
求椭圆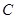 的方程;
的方程;
设椭圆的上顶点为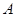 ,过点
,过点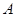 作椭圆
作椭圆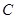 的两条动弦
的两条动弦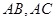 ,若直线
,若直线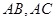 斜率之积为
斜率之积为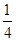 ,直线
,直线 是否一定经过一定点?若经过,求出该定点坐标;若不经过,请说明理由.
是否一定经过一定点?若经过,求出该定点坐标;若不经过,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com