
【题目】在平面直角坐标系![]() 中,点集
中,点集![]() ,在
,在![]() 中随机取出三个点,则这三个点两两之间距离不超过2的概率为________
中随机取出三个点,则这三个点两两之间距离不超过2的概率为________
【答案】![]()
【解析】
点集![]() 中有9个点,从而在
中有9个点,从而在![]() 中随机取出三个点的方式数为
中随机取出三个点的方式数为![]() ,当取出的三个点两两之间的距离不超过2时,有如下三种情况:三点在一横线或一纵线上,有6种情况,三点是1,1,
,当取出的三个点两两之间的距离不超过2时,有如下三种情况:三点在一横线或一纵线上,有6种情况,三点是1,1,![]() 的等腰直角三角形的顶点,有
的等腰直角三角形的顶点,有![]() 种情况,三点是边长为
种情况,三点是边长为![]() 的等腰直角三角形的顶点,有8种情况,由此能求出这三个点两两之间距离均不超过2的概率.
的等腰直角三角形的顶点,有8种情况,由此能求出这三个点两两之间距离均不超过2的概率.
![]() 在平面直角坐标系
在平面直角坐标系![]() 中,点集
中,点集![]() ,
,
∴![]() 中有9个点,
中有9个点,![]() 在
在![]() 中随机取出三个点的方式数为
中随机取出三个点的方式数为![]() ,
,
当取出的三个点两两之间的距离不超过2时,有如下三种情况:
①三点在一横线或一纵线上,有6种情况,
②三点是边长为1,1,![]() 的等腰直角三角形的顶点,有
的等腰直角三角形的顶点,有![]() 种情况,
种情况,
③三点是边长为![]() ,
,![]() ,
,![]() 的等腰直角三角形的顶点,
的等腰直角三角形的顶点,
其中,直角顶点位于![]() 的有4个,直角顶点位于
的有4个,直角顶点位于![]() ,
,![]() 的各有1个,
的各有1个,
共有8种情况,
综上,选出的三点两两之间距离不超过2的情况数为![]() ,
,
![]() 这三个点两两之间距离均不超过2的概率为
这三个点两两之间距离均不超过2的概率为![]() .
.
故答案为:![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,
中,![]() 底面
底面![]() ,底面
,底面![]() 为平行四边形,
为平行四边形,![]() ,且
,且![]() ,
,![]() ,
,![]() 是棱
是棱![]() 的中点.
的中点.
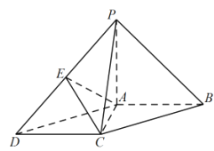
(1)求证:![]() 平面
平面![]() ;
;
(2)求直线![]() 与平面
与平面![]() 所成角的正弦值;
所成角的正弦值;
(3)在线段![]() 上(不含端点)是否存在一点
上(不含端点)是否存在一点![]() ,使得二面角
,使得二面角![]() 的余弦值为
的余弦值为![]() ?若存在,确定
?若存在,确定![]() 的位置;若不存在,请说明理由.
的位置;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为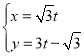 (
(![]() 为参数),以坐标原点为极点,
为参数),以坐标原点为极点,![]() 轴的非负半轴为极轴且取相同的单位长度建立极坐标系,曲线
轴的非负半轴为极轴且取相同的单位长度建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 的极坐标方程和曲线
的极坐标方程和曲线![]() 的参数方程;
的参数方程;
(2)若![]() ,直线
,直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,求
两点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了治理空气污染,某市设![]() 个监测站用于监测空气质量指数
个监测站用于监测空气质量指数![]() ,其中在轻度污染区、中度污染区、重度污染区分别设有
,其中在轻度污染区、中度污染区、重度污染区分别设有![]() 、
、![]() 、
、![]() 个监测站,并以
个监测站,并以![]() 个监测站测得的
个监测站测得的![]() 的平均值为依据播报该市的空气质量.
的平均值为依据播报该市的空气质量.
(1)若某日播报的![]() 为
为![]() ,已知轻度污染区
,已知轻度污染区![]() 平均值为
平均值为![]() ,中度污染区
,中度污染区![]() 平均值为
平均值为![]() ,求重试污染区
,求重试污染区![]() 平均值;
平均值;
(2)如图是![]() 年
年![]() 月份
月份![]() 天的
天的![]() 的频率分布直方图,
的频率分布直方图,![]() 月份仅有
月份仅有![]() 天
天![]() 在
在![]() 内.
内.
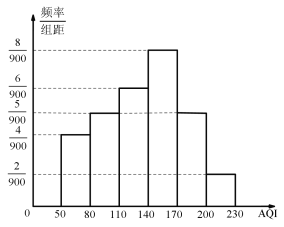
①某校参照官方公布的![]() ,如果周日
,如果周日![]() 小于
小于![]() 就组织学生参加户外活动,以统计数据中的频率为概率,求该校学生周日能参加户外活动的概率;
就组织学生参加户外活动,以统计数据中的频率为概率,求该校学生周日能参加户外活动的概率;
②环卫部门从![]() 月份
月份![]() 不小于
不小于![]() 的数据中抽取两天的数据进行研究,求抽取的这两天中
的数据中抽取两天的数据进行研究,求抽取的这两天中![]() 值都在
值都在![]() 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出以下三个条件:
①数列![]() 是首项为 2,满足
是首项为 2,满足![]() 的数列;
的数列;
②数列![]() 是首项为2,满足
是首项为2,满足![]() (λ∈R)的数列;
(λ∈R)的数列;
③数列![]() 是首项为2,满足
是首项为2,满足![]() 的数列..
的数列..
请从这三个条件中任选一个将下面的题目补充完整,并求解.
设数列![]() 的前n项和为
的前n项和为![]() ,
,![]() 与
与![]() 满足______,记数列
满足______,记数列![]() ,
,![]() ,求数列{
,求数列{![]() }的前n项和
}的前n项和![]() ;
;
(注:如选择多个条件分别解答,按第一个解答计分)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,
为极点,![]() 轴非负半轴为极轴建立极坐标系,点
轴非负半轴为极轴建立极坐标系,点![]() 为曲线
为曲线![]() 上的动点,点
上的动点,点![]() 在线段
在线段![]() 的延长线上且满足
的延长线上且满足![]() 点
点![]() 的轨迹为
的轨迹为![]() .
.
(1)求曲线![]() 的极坐标方程;
的极坐标方程;
(2)设点![]() 的极坐标为
的极坐标为![]() ,求
,求![]() 面积的最小值.
面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (k为常数,
(k为常数,![]() 且
且![]() ).
).
(1)在下列条件中选择一个________使数列![]() 是等比数列,说明理由;
是等比数列,说明理由;
①数列![]() 是首项为2,公比为2的等比数列;
是首项为2,公比为2的等比数列;
②数列![]() 是首项为4,公差为2的等差数列;
是首项为4,公差为2的等差数列;
③数列![]() 是首项为2,公差为2的等差数列的前n项和构成的数列.
是首项为2,公差为2的等差数列的前n项和构成的数列.
(2)在(1)的条件下,当![]() 时,设
时,设![]() ,求数列
,求数列![]() 的前n项和
的前n项和![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com