
【题目】选修4-4:坐标系与参数方程
在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),在以坐标原点为极点,
为参数),在以坐标原点为极点,![]() 轴正半轴为极轴的极坐标系中,直线
轴正半轴为极轴的极坐标系中,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 和直线
和直线![]() 在该直角坐标系下的普通方程;
在该直角坐标系下的普通方程;
(2)动点![]() 在曲线
在曲线![]() 上,动点
上,动点![]() 在直线
在直线![]() 上,定点
上,定点![]() 的坐标为
的坐标为![]() ,求
,求![]() 的最小值.
的最小值.
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的离心率为
的离心率为![]() ,以短轴端点和焦点为顶点的四边形的周长为
,以短轴端点和焦点为顶点的四边形的周长为![]() .
.
(Ⅰ)求椭圆![]() 的标准方程及焦点坐标.
的标准方程及焦点坐标.
(Ⅱ)过椭圆![]() 的右焦点作
的右焦点作![]() 轴的垂线,交椭圆于
轴的垂线,交椭圆于![]() 、
、![]() 两点,过椭圆上不同于点
两点,过椭圆上不同于点![]() 、
、![]() 的任意一点
的任意一点![]() ,作直线
,作直线![]() 、
、![]() 分别交
分别交![]() 轴于
轴于![]() 、
、![]() 两点.证明:点
两点.证明:点![]() 、
、![]() 的横坐标之积为定值.
的横坐标之积为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线C:![]() =2px(p>0)的准线方程为x=-
=2px(p>0)的准线方程为x=-![]() ,F为抛物线的焦点
,F为抛物线的焦点
(I)求抛物线C的方程;
(II)若P是抛物线C上一点,点A的坐标为(![]() ,2),求
,2),求![]() 的最小值;
的最小值;
(III)若过点F且斜率为1的直线与抛物线C交于M,N两点,求线段MN的中点坐标。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() 为抛物线
为抛物线![]() 的焦点,
的焦点,![]() 为抛物线
为抛物线![]() 上三点,且点
上三点,且点![]() 在第一象限,直线
在第一象限,直线![]() 经过点
经过点![]() 与抛物线
与抛物线![]() 在点
在点![]() 处的切线平行,点
处的切线平行,点![]() 为
为![]() 的中点.
的中点.
(1)证明:![]() 与
与![]() 轴平行;
轴平行;
(2)求![]() 面积
面积![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某手机生产厂商为迎接5G时代的到来,要生产一款5G手机,在生产之前,该公司对手机屏幕的需求尺寸进行社会调查,共调查了400人,将这400人按对手机屏幕的需求尺寸分为6组,分别是:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() (单位:英寸),得到如下频率分布直方图:
(单位:英寸),得到如下频率分布直方图:

其中,屏幕需求尺寸在![]() 的一组人数为50人.
的一组人数为50人.
(1)求a和b的值;
(2)用分层抽样的方法在屏幕需求尺寸为![]() 和
和![]() 两组人中抽取6人参加座谈,并在6人中选择2人做代表发言,则这2人来自同一分组的概率是多少?
两组人中抽取6人参加座谈,并在6人中选择2人做代表发言,则这2人来自同一分组的概率是多少?
(3)若以厂家此次调查结果的频率作为概率,市场随机调查两人,这两人屏幕需求尺寸分别在![]() 和
和![]() 的概率是多少?
的概率是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解甲、乙两种离子在小鼠体内的残留程度,进行如下试验:将200只小鼠随机分成![]() 两组,每组100只,其中
两组,每组100只,其中![]() 组小鼠给服甲离子溶液,
组小鼠给服甲离子溶液,![]() 组小鼠给服乙离子溶液.每只小鼠给服的溶液体积相同、摩尔浓度相同.经过一段时间后用某种科学方法测算出残留在小鼠体内离子的百分比.根据试验数据分别得到如下直方图:
组小鼠给服乙离子溶液.每只小鼠给服的溶液体积相同、摩尔浓度相同.经过一段时间后用某种科学方法测算出残留在小鼠体内离子的百分比.根据试验数据分别得到如下直方图:

记![]() 为事件:“乙离子残留在体内的百分比不低于
为事件:“乙离子残留在体内的百分比不低于![]() ”,根据直方图得到
”,根据直方图得到![]() 的估计值为
的估计值为![]() .
.
(1)求乙离子残留百分比直方图中![]() 的值;
的值;
(2)分别估计甲、乙离子残留百分比的平均值(同一组中的数据用该组区间的中点值为代表).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】数列{an}中的项按顺序可以排成如图的形式,第一行1项,排a1;第二行2项,从左到右分别排a2,a3;第三行3项,……依此类推,设数列{an}的前n项和为Sn,则满足Sn>2019的最小正整数n的值为()

A. 20B. 21C. 26D. 27
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市规定,高中学生在校期间须参加不少于80小时的社区服务才合格.某校随机抽取20位学生参加社区服务的数据,按时间段![]() (单位:小时)进行统计,其频率分布直方图如图所示.
(单位:小时)进行统计,其频率分布直方图如图所示.
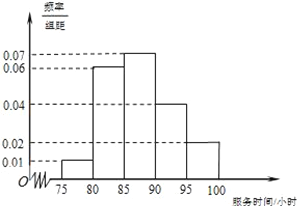
(1)求抽取的20人中,参加社区服务时间不少于90小时的学生人数;
(2)从参加社区服务时间不少于90小时的学生中任意选取2人,求所选学生的参加社区服务时间在同一时间段内的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某闯关游戏规划是:先后掷两枚骰子,将此试验重复![]() 轮,第
轮,第![]() 轮的点数分别记为
轮的点数分别记为![]() ,如果点数满足
,如果点数满足![]() ,则认为第
,则认为第![]() 轮闯关成功,否则进行下一轮投掷,直到闯关成功,游戏结束.
轮闯关成功,否则进行下一轮投掷,直到闯关成功,游戏结束.
(1)求第1轮闯关成功的概率;
(2)如果第![]() 轮闯关成功所获的奖金(单位:元)
轮闯关成功所获的奖金(单位:元) ![]() ,求某人闯关获得奖金不超过2500元的概率;
,求某人闯关获得奖金不超过2500元的概率;
(3)如果游戏只进行到第4轮,第4轮后无论游戏成功与否,都终止游戏,记进行的轮数为随机变量![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com