
(本小题15分)
设数列{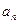 }的前n项和为
}的前n项和为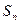 ,并且满足
,并且满足 ,
,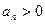 (n∈N*).
(n∈N*).
(Ⅰ)求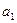 ,
,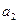 ,
,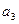 ;
;
(Ⅱ)猜想{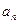 }的通项公式,并用数学归纳法加以证明;
}的通项公式,并用数学归纳法加以证明;
(Ⅲ)设 ,
,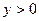 ,且
,且 ,证明:
,证明: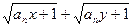 ≤
≤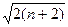 .
.
 通城学典默写能手系列答案
通城学典默写能手系列答案科目:高中数学 来源:2011届山东省莱芜市一中高三上学期期末考试数学文卷 题型:解答题
(本小题满分12分)
某班全部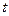 名学生在一次百米测试中,成绩全部介于13秒和18秒之间。将测试结果按如下方式分为五组:第一组[13,14);第二组[14,15);…;第五组[17,18],表是
名学生在一次百米测试中,成绩全部介于13秒和18秒之间。将测试结果按如下方式分为五组:第一组[13,14);第二组[14,15);…;第五组[17,18],表是 按上述分组方式得到的频率分布表。
按上述分组方式得到的频率分布表。
| 分 组 | 频数 | 频率 |
| [13,14) |  | 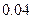 |
| [14,15) | 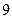 | 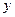 |
| [15,16) | 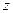 |  |
| [16,17) | 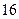 | 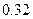 |
| [17,18] | 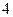 | 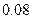 |
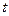 及上表中的
及上表中的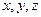 的值;
的值; 百米测试成绩,求事件“
百米测试成绩,求事件“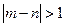 ”的
”的 概率.
概率.查看答案和解析>>
科目:高中数学 来源:2012-2013学年福建省泉州市高三毕业班质量检查理科数学试卷(解析版) 题型:解答题
(本小题满分13分)
甲、乙两台机床生产同一型号零件.记生产的零件的尺寸为 (cm),相关行业质检部门规定:若
(cm),相关行业质检部门规定:若 ,则该零件为优等品;若
,则该零件为优等品;若 ,则该零件为中等品;其余零件为次品.现分别从甲、乙机床生产的零件中各随机抽取50件,经质量检测得到下表数据:
,则该零件为中等品;其余零件为次品.现分别从甲、乙机床生产的零件中各随机抽取50件,经质量检测得到下表数据:
|
尺寸 |
|
|
|
|
|
|
|
甲机床零件频数 |
2 |
3 |
20 |
20 |
4 |
1 |
|
乙机床零件频数 |
3 |
5 |
17 |
13 |
8 |
4 |
(Ⅰ)设生产每件产品的利润为:优等品3元,中等品1元,次品亏本1元. 若将频率视为概率,试根据样本估计总体的思想,估算甲机床生产一件零件的利润的数学期望;
(Ⅱ)对于这两台机床生产的零件,在排除其它因素影响的情况下,试根据样本估计总体的思想,估计约有多大的把握认为“零件优等与否和所用机床有关”,并说明理由.
参考公式: .
.
参考数据:
|
|
0.25 |
0.15 |
0.10 |
0.05 |
0.025 |
0.010 |
|
|
1.323 |
2.072 |
2.706 |
3.841 |
5.024 |
6.635 |
查看答案和解析>>
科目:高中数学 来源:2011-2012学年福建省漳州市四地七校高三第四次联考理科数学试卷(解析版) 题型:解答题
(本小题满分13分)对某校高一年级的学生参加社区服务的次数进行统计,随机抽取M名学生作为样本,得到这M名学生参加社区服务的次数,根据此数据作出了下图所示的频数与频率的统计表和频率分布直方图:

(I)求出表中M、p及图中a的值
(II)学校决定对参加社区服务的学生进行表彰,对参加活动次数在[25,30]区间的每个学生发放价值80元的学习用品,对参加活动次数在[20,25)区间的每个学生发放价值60元的学习用品,对参加活动次数在[15,20)区间的每个学生发放价值40元的学习用品,对参加活动次数在[10,15)区间的每个学生发放价值20元的学习用品,在所抽取的这M名学生中,任意取出2人,设X为此二人所获得学习用品价值之差的绝对值,求X的分布列与数学期望E(X)。
查看答案和解析>>
科目:高中数学 来源:2010-2011学年山东省莱芜市高三上学期期末考试数学文卷 题型:解答题
(本小题满分12分)
某班全部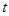 名学生在一次百米测试中,成绩全部介于13秒和18秒之间。将测试结果按如下方式分为五组:第一组[13,14);第二组[14,15);…;第五组[17,18],表是按上述分组方式得到的频率分布表。
名学生在一次百米测试中,成绩全部介于13秒和18秒之间。将测试结果按如下方式分为五组:第一组[13,14);第二组[14,15);…;第五组[17,18],表是按上述分组方式得到的频率分布表。
|
分 组 |
频数 |
频率 |
|
[13,14) |
|
|
|
[14,15) |
|
|
|
[15,16) |
|
|
|
[16,17) |
|
|
|
[17,18] |
|
|
(1)求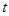 及上表中的
及上表中的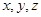 的值;
的值;
(2)设m,n是从第一组或第五组中任意抽取的两名学生的百米测试成绩,求事件“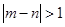 ”的概率.
”的概率.
查看答案和解析>>
科目:高中数学 来源:2010-2011学年山东省莱芜市高三上学期期末考试数学文卷 题型:解答题
(本小题满分12分)
某班全部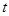 名学生在一次百米测试中,成绩全部介于13秒和18秒之间。将测试结果按如下方式分为五组:第一组[13,14);第二组[14,15);…;第五组[17,18],表是按上述分组方式得到的频率分布表。
名学生在一次百米测试中,成绩全部介于13秒和18秒之间。将测试结果按如下方式分为五组:第一组[13,14);第二组[14,15);…;第五组[17,18],表是按上述分组方式得到的频率分布表。
|
分 组 |
频数 |
频率 |
|
[13,14) |
|
|
|
[14,15) |
|
|
|
[15,16) |
|
|
|
[16,17) |
|
|
|
[17,18] |
|
|
(1)求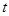 及上表中的
及上表中的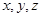 的值;
的值;
(2)设m,n是从第一组或第五组中任意抽取的两名学生的百米测试成绩,求事件“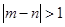 ”的概率.
”的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com