【题目】某篮球队有
名队员，其中有
名队员打前锋，有
名队员打后卫，甲、乙两名队员既能打前锋又能打后卫.若出场阵容为
名前锋，
名后卫，则不同的出场阵容共有______种．
【答案】
【解析】
分三种情况讨论：①甲、乙都不出场；②甲、乙只有一人出场；③甲、乙都出场.分别计算出每种情况下出场的阵容种数，利用分类加法计数原理即可得出结果.
分以下三种情况讨论：
①甲、乙都不出场，则应从
名打前锋的队员中挑选
人，从
名打后卫的队员中挑选
人，此时，出场阵容种数为
；
②甲、乙只有一人出场，若出场的这名队员打前锋，则应从名打前锋的队员中挑选人，从名打后卫的队员中挑选人；若出场的这名队员打后卫，则应从名打前锋的队员中挑选人，从名打后卫的队员中挑选
人.
此时，出场阵容种数为
；
③甲、乙都出场，若这两名队员都打前锋，则应从名打前锋的队员中挑选人，从名打后卫的队员中挑选人；若这两名队员都打后卫，则应从名打前锋的队员中挑选人，从名打后卫的队员中不用挑选；若这两名队员一人打前锋、一人打后卫，则应从名打前锋的队员中挑选人，从名打后卫的队员中挑选人，此时，出场阵容种数为
.
综上所述，由分类加法计数原理可知，共有
种不同的出场阵容.
故答案为：.
科目：高中数学 来源： 题型：
【题目】已知椭圆
，四点
，
，
，
中恰有三点在椭圆
上.
（I）求椭圆的标准方程；
（Ⅱ）过的右焦点
作斜率为
的直线
与交于
，
两点，直线
与
轴交于点
，
为线段
的中点，过点作直线
于点
.证明：，，三点共线.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知椭圆
：
的左、右焦点分别为
、
，过的直线
与椭圆相交于
、
两点．
（1）求
的周长；
（2）设点
为椭圆的上顶点，点在第一象限，点
在线段
上．若
，求点的横坐标；
（3）设直线不平行于坐标轴，点
为点关于
轴的对称点，直线
与轴交于点
．求
面积的最大值．
查看答案和解析>>
科目：高中数学 来源： 题型：
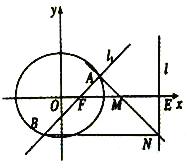
【题目】抛物线M:
的焦点为F，过焦点F的直线l(与x轴不垂直)交抛物线M于点A，B，A关于x轴的对称点为
.
(1)求证:直线
过定点，并求出这个定点；
(2)若的垂直平分线交抛物线于C，D，四边形
外接圆圆心N的横坐标为19，求直线AB和圆N的方程.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数f（x）＝ln（x2+1）﹣e﹣|x|（e为自然对数的底数），则不等式f（2x+1）＞f（x）的解集是（ ）
A. （﹣1，1）B. （﹣∞，﹣1）∪（1，+∞）
C. 
D. 
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】（本小题满分12分）
某高校设计了一个实验学科的实验考查方案：考生从6道备选题中一次性随机抽取3题，按照题目要求独立完成全部实验操作。规定：至少正确完成其中2题的便可提交通过。已知6道备选题中考生甲有4道题能正确完成，2道题不能完成；考生乙每题正确完成的概率都是
，且每题正确完成与否互不影响。
（Ⅰ）分别写出甲、乙两考生正确完成题数的概率分布列，并计算数学期望；
（Ⅱ）试从两位考生正确完成题数的数学期望及至少正确完成2题的概率分析比较两位考生的实验操作能力．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在同一直角坐标系中，经过伸缩变换
后，曲线C的方程变为
.以坐标原点为极点，x轴正半轴为极轴建立极坐标系，直线/的极坐标方程为
.
（1）求曲线C和直线l的直角坐标方程；
（2）过点
作l的垂线l0交C于A，B两点，点A在x轴上方，求
的值.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】2021年福建省高考实行“
”模式.“”模式是指：“3”为全国统考科目语文、数学、外语，所有学生必考；“1”为首选科目，考生须在高中学业水平考试的物理、历史科目中选择1科；“2”为再选科目，考生可在化学、生物、政治、地理4个科目中选择2科，共计6个考试科目.
（1）若学生甲在“1”中选物理，在“2”中任选2科，求学生甲选化学和生物的概率；
（2）若学生乙在“1”中任选1科，在“2”中任选2科，求学生乙不选政治但选生物的概率.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在直角坐标系
中，直线
的参数方程为
（
为参数），以坐标原点为极点，
轴的正半轴为极轴建立极坐标系，曲线
的极坐标方程为
.
（1）写出直线的直角坐标方程；
（2）设点
的坐标为
，若点是曲线截直线所得线段的中点，求的斜率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com