
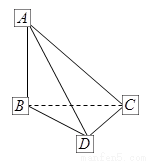
如图所示,在四面体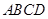 中,
中,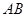 ,
,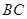 ,
,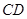 两两互相垂直,且
两两互相垂直,且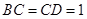 .
.
(1)求证:平面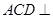 平面
平面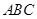 ;
;
(2)求二面角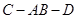 的大小;
的大小;
(3)若直线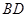 与平面
与平面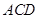 所成的角为
所成的角为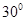 ,求线段
,求线段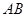 的长度.
的长度.
(1)见解析 (2)二面角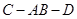 的大小为
的大小为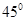 . (3)
. (3)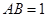 .
.
【解析】本题考查平面与平面垂直的判定,直线与平面所成的角,二面角及其度量,考查逻辑思维能力,转化思想,是中档题.熟练掌握空间线面关系的判定定理及性质定理,及线面夹角和二面角的定义是解答此类问题的关键.
(Ⅰ)要证平面ACD⊥平面ABC,只需证明平面ACD内的直线CD,垂直平面ABC内的两条相交直线AB,BC,即可证明CD⊥平面ABC,从而证明平面ACD⊥平面ABC.
(Ⅱ)说明∠CBD是二面角C-AB-D的平面角,解Rt△BCD,求二面角C-AB-D的大小;
(Ⅲ)过点B作BH⊥AC,垂足为H,连接DH,则∠BDH为BD与平面ACD所成的角,解Rt△BHD即可确定∠BDH正弦值的范围,进而得到AB


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
 15、如图所示,在四面体ABCD中,E,F,G分别是棱AB,AC,CD的中点,则过E,F,G的截面把四面体分成两部分的体积之比VADEFGH:VBCEFGH=
15、如图所示,在四面体ABCD中,E,F,G分别是棱AB,AC,CD的中点,则过E,F,G的截面把四面体分成两部分的体积之比VADEFGH:VBCEFGH=查看答案和解析>>
科目:高中数学 来源:2012-2013学年湖北省高三最后一次综合测试数学试卷(解析版) 题型:解答题
如图所示,在四面体 中,
中, ,
, ,
, 两两互相垂直,且
两两互相垂直,且 .
.

(1)求证:平面 平面
平面 ;
;
(2)求二面角 的大小;
的大小;
(3)若直线 与平面
与平面 所成的角为
所成的角为 ,求线段
,求线段 的长度.
的长度.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年湖南省长望浏宁四市县区高三5月联考文科数学试卷(解析版) 题型:解答题
如图所示,在四面体 中,
中, ,
, ,
, 两两互相垂直,且
两两互相垂直,且 .
.

(1)求证:平面 平面
平面 ;
;
(2)求二面角 的大小;
的大小;
(3)若直线 与平面
与平面 所成的角为
所成的角为 ,求线段
,求线段 的长度.
的长度.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年广东揭阳一中、潮州金山中学高三第三次模拟考试理科数学试卷(解析版) 题型:解答题
(14分)如图所示,在四面体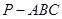 中,已知
中,已知
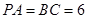 ,
,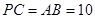 ,
,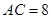 ,
,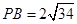 ,
, 是线段
是线段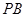 上一点,
上一点,
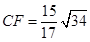 ,点
,点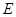 在线段
在线段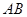 上,且
上,且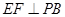 。
。
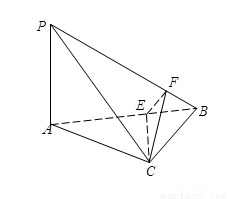
⑴证明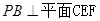 ;
;
⑵求二面角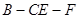 的平面角的正弦值。
的平面角的正弦值。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com