
【题目】如图,在四棱锥![]() 中,
中,![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 为
为![]() 的中点.
的中点.
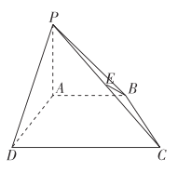
(1)求证:![]() 平面
平面![]() ;
;
(2)求三棱锥![]() 的体积.
的体积.
【答案】(1)证明见解析;(2)![]()
【解析】
(1)取![]() 的中点
的中点![]() ,先证明四边形
,先证明四边形![]() 是平行四边形,可得
是平行四边形,可得![]() ,只需证
,只需证![]() 平面
平面![]() 即可,而由已知易证
即可,而由已知易证![]() 平面
平面![]() ,从而可证得
,从而可证得![]() ,而由等腰三角形的性质可证得
,而由等腰三角形的性质可证得![]() ,由此可证得
,由此可证得![]() 平面
平面![]() ;
;
(2)先在![]() 中利用勾股定理求出
中利用勾股定理求出![]() 的长,再在
的长,再在![]() 中,求出
中,求出![]() ,从而可得
,从而可得![]() 的长,而
的长,而![]() 为
为![]() 的中点,所以
的中点,所以![]() ,在
,在![]() 中,再利用勾股定理求出
中,再利用勾股定理求出![]() ,而由(1)可知
,而由(1)可知![]() 平面
平面![]() ,所以
,所以![]() ,代值可得答案.
,代值可得答案.
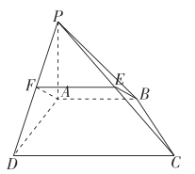
(1)证明:如下图,取![]() 的中点
的中点![]() ,连接
,连接![]() ,
,![]() .
.
又![]() 为
为![]() 的中点,则
的中点,则![]() 是
是![]() 的中位线.
的中位线.
所以![]() 且
且![]() .
.
又![]() 且
且![]() ,
,
所以![]() 且
且![]() .
.
所以四边形![]() 是平行四边形.
是平行四边形.
所以![]() .
.
因为![]() ,
,![]() 为
为![]() 的中点,
的中点,
所以![]() .
.
因为![]() ,
,![]() ,
,
所以![]() .
.
因为![]() 平面
平面![]() ,所以
,所以![]() .
.
又![]() ,所以
,所以![]() 平面
平面![]() .
.
所以![]() .
.
又![]() ,所以
,所以![]() 平面
平面![]() .
.
又![]() ,所以
,所以![]() 平面
平面![]() .
.
(2)因为![]() ,
,
所以由勾股定理得![]() ,
,![]() ,
,![]() .
.
所以![]() .
.
所以![]() .
.
由(1)得,![]() 平面
平面![]() ,所以
,所以![]() .
.
所以![]() .
.
由(1)得,![]() 平面
平面![]() ,
,
所以![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】某饲料厂原有陈粮10吨,又购进新粮x吨,现将粮食总库存量的一半精加工为饲料.若被精加工的新粮最多可用![]() 吨,被精加工的陈粮最多可用y2吨,记
吨,被精加工的陈粮最多可用y2吨,记![]() ,则函数
,则函数![]() 的图象为( )
的图象为( )
A.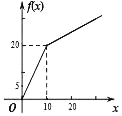 B.
B.
C.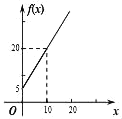 D.
D.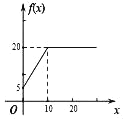
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 的焦点为
的焦点为![]() ,
,![]() 轴上方的点
轴上方的点![]() 在抛物线上,且
在抛物线上,且![]() ,直线
,直线![]() 与抛物线交于
与抛物线交于![]() ,
,![]() 两点(点
两点(点![]() ,
,![]() 与
与![]() 不重合),设直线
不重合),设直线![]() ,
,![]() 的斜率分别为
的斜率分别为![]() ,
,![]() .
.
(Ⅰ)求抛物线的方程;
(Ⅱ)当![]() 时,求证:直线
时,求证:直线![]() 恒过定点并求出该定点的坐标.
恒过定点并求出该定点的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】关于函数![]()
(1)![]() 是
是![]() 的极小值点;
的极小值点;
(2)函数![]() 有且只有1个零点;
有且只有1个零点;
(3)![]() 恒成立;
恒成立;
(4)设函数![]() ,若存在区间
,若存在区间![]() ,使
,使![]() 在
在![]() 上的值域是
上的值域是![]() ,则
,则![]() .
.
上述说法正确的序号为_______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从某小区抽取50户居民进行月用电量调查,发现其用电量都在50到350度之间,将用电量的数据绘制成频率分布直方图如下.
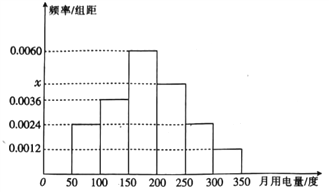
(1)求频率分布直方图中![]() 的值并估计这50户用户的平均用电量;
的值并估计这50户用户的平均用电量;
(2)若将用电量在区间![]() 内的用户记为
内的用户记为![]() 类用户,标记为低用电家庭,用电量在区间
类用户,标记为低用电家庭,用电量在区间![]() 内的用户记为
内的用户记为![]() 类用户,标记为高用电家庭,现对这两类用户进行问卷调查,让其对供电服务进行打分,打分情况见茎叶图:
类用户,标记为高用电家庭,现对这两类用户进行问卷调查,让其对供电服务进行打分,打分情况见茎叶图:
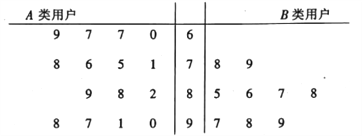
①从![]() 类用户中任意抽取3户,求恰好有2户打分超过85分的概率;
类用户中任意抽取3户,求恰好有2户打分超过85分的概率;
②若打分超过85分视为满意,没超过85分视为不满意,请填写下面列联表,并根据列联表判断是否有![]() 的把握认为“满意度与用电量高低有关”?
的把握认为“满意度与用电量高低有关”?
满意 | 不满意 | 合计 | |
| |||
| |||
合计 |
附表及公式:
| <>0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
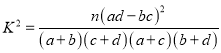 ,
, ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设一个袋子里有红、黄、蓝色小球各一个现每次从袋子里取出一个球(取出某色球的概率均相同),确定颜色后放回,直到连续两次均取出红色球时为止,记此时取出球的次数为ξ,则ξ的数学期望为_____ .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AB∥CD,AB⊥AD,PA⊥平面ABCD,E是棱PC上一点.

(1)证明:平面ADE⊥平面PAB.
(2)若PE=4EC,O为点E在平面PAB上的投影,![]() ,AB=AP=2CD=2,求四棱锥P-ADEO的体积.
,AB=AP=2CD=2,求四棱锥P-ADEO的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的离心率为
的离心率为![]() ,左、右焦点分别为
,左、右焦点分别为![]() ,点
,点![]() 在椭圆
在椭圆![]() 上,
上,![]() 的周长为
的周长为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)已知直线l经过点![]() ,且与椭圆
,且与椭圆![]() 交于不同的两点
交于不同的两点![]() ,若
,若![]() (
(![]() 为坐标原点)成等比数列,判断直线
为坐标原点)成等比数列,判断直线![]() 的斜率是否为定值?若是,请求出该定值;若不是,请说明理由.
的斜率是否为定值?若是,请求出该定值;若不是,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com