
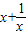 的图象为c1,c1关于点A(2,1)对称的图象为c2,c2对应的函数为g(x)
的图象为c1,c1关于点A(2,1)对称的图象为c2,c2对应的函数为g(x)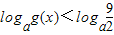 (a>0且≠1)
(a>0且≠1)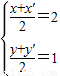 ,解得x'=4-x,y'=2-y,即P'(4-x,2-y),
,解得x'=4-x,y'=2-y,即P'(4-x,2-y),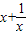 的图象c1上,∴2-y=4-x+
的图象c1上,∴2-y=4-x+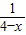 ,则y=
,则y=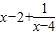 ,
,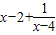 .
.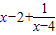 >0,即
>0,即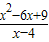 >0,
>0,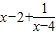 <
< ,即
,即 -
- <0,
<0,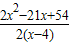 <0,
<0, <x<6;
<x<6;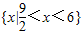 ,
,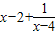 >
> ,即
,即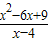 -
- >0,
>0,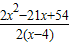 >0,
>0, ,
, 或x>6,即不等式的解集是
或x>6,即不等式的解集是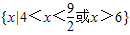 ,
,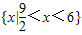 ,
,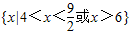 .
.

 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:高中数学 来源: 题型:
| π | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| lnx |
| x |
| 1 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| lnx |
| x |
| 1 |
| 2 |
| x |
| m |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 个单位,可得曲线C2,若曲线C2与函数y=cos2x的图象关于x轴对称,那么f(x)可以是________.
个单位,可得曲线C2,若曲线C2与函数y=cos2x的图象关于x轴对称,那么f(x)可以是________.查看答案和解析>>
科目:高中数学 来源:2011年高三数学复习(第3章 三角函数与三角恒等变换):3.3 三角函数的图象(解析版) 题型:解答题
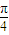 个单位,可得曲线C2,若曲线C2与函数y=cos2x的图象关于x轴对称,那么f(x)可以是 .
个单位,可得曲线C2,若曲线C2与函数y=cos2x的图象关于x轴对称,那么f(x)可以是 .查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com