Question

【题目】在矩形ABCD中，AB=1，AD=2，动点P在以点C为圆心且与BD相切的圆上．若= + ，则+的最大值为__________．

Answer 1

【答案】

【解析】分析：如图：以A为原点，以AB，AD所在的直线为x，y轴建立如图所示的坐标系，先求出圆的标准方程，再设点P的坐标为（cosθ+1，sinθ+2），根据=λ+μ，求出λ，μ，根据三角函数的性质即可求出最值．

详解：如图：以A为原点，以AB，AD所在的直线为x，y轴建立如图所示的坐标系，

则A（0，0），B（1，0），D（0，2），C（1，2），

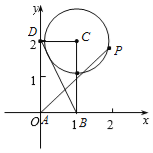
∵动点P在以点C为圆心且与BD相切的圆上，

设圆的半径为r，

∵BC=2，CD=1，

∴BD==

∴BCCD=BDr，

∴r=，

∴圆的方程为（x﹣1）2+（y﹣2）2=，

设点P的坐标为（cosθ+1，sinθ+2），

∵=λ+μ，

∴（cosθ+1，sinθ+2）=λ（1，0）+μ（0，2）=（λ，2μ），

∴cosθ+1=λ，sinθ+2=2μ，

∴λ+μ=cosθ+sinθ+2=sin（θ+φ）+2，其中tanφ=2，

∵﹣1≤sin（θ+φ）≤1，

∴1≤λ+μ≤3，

故λ+μ的最大值为3，

故答案为：3．